Question

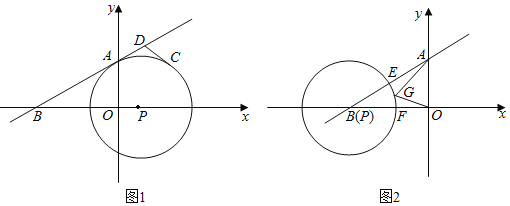
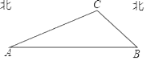
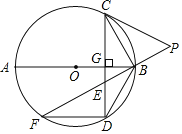
【题目】如图，AB为⊙O的直径，CD⊥AB于点G，E是CD上一点，且BE＝DE，延长EB至点P，连接CP，使PC＝PE，延长BE与⊙O交于点F，连结BD，FD．

（1）连结BC，求证：△BCD≌△DFB；

（2）求证：PC是⊙O的切线；

（3）若tanF＝，AG﹣BG＝，求ED的值．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）DE＝．

【解析】

（1）由BE=DE可知∠CDB=∠FBD，而∠BFD=∠DCB，BD是公共边，结论显然成立．

（2）连接OC，只需证明OC⊥PC即可．根据三角形外角知识以及圆心角与圆周角关系可知∠PEC=2∠CDB=∠COB，由PC=PE可知∠PCE=∠PEC=∠COB，注意到AB⊥CD，于是∠COB+∠OCG=90°=∠OCG+∠PEC=∠OCP，结论得证．

（3）由于∠BCD=∠F，于是tan∠BCD=tanF=，设BG=2x，则CG=3x．注意到AB是直径，连接AC，则∠ACB是直角，由射影定理可知CG2=BGAG，可得出AG的表达式（用x表示），再根据AG-BG=求出x的值，从而CG、CB、BD、CD的长度可依次得出，最后利用△DEB∽△DBC列出比例关系算出ED的值．

解：（1）证明：因为BE＝DE，

所以∠FBD＝∠CDB，

在△BCD和△DFB中：

∠BCD＝∠DFB

∠CDB＝∠FBD

BD＝DB

所以△BCD≌△DFB（AAS）．

（2）证明：连接OC．

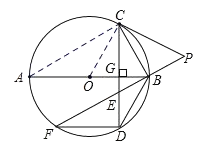
因为∠PEC＝∠EDB+∠EBD＝2∠EDB，

∠COB＝2∠EDB，

所以∠COB＝∠PEC，

因为PE＝PC，

所以∠PEC＝∠PCE，

所以∠PCE＝∠COB，

因为AB⊥CD于G，

所以∠COB+∠OCG＝90°，

所以∠OCG+∠PEC＝90°，

即∠OCP＝90°，

所以OC⊥PC，

所以PC是圆O的切线．

（3）因为直径AB⊥弦CD于G，

所以BC＝BD，CG＝DG，

所以∠BCD＝∠BDC，

因为∠F＝∠BCD，tanF＝，

所以∠tan∠BCD＝＝，

设BG＝2x，则CG＝3x．

连接AC，则∠ACB＝90°，

由射影定理可知：CG2＝AGBG，

所以AG＝，

因为AG﹣BG＝，

所以，

解得x＝，

所以BG＝2x＝，CG＝3x＝，

所以BC＝，

所以BD＝BC＝，

因为∠EBD＝∠EDB＝∠BCD，

所以△DEB∽△DBC，

所以，

因为CD＝2CG＝，

所以DE＝．