题目内容
关于x的一元二次方程x2+2(m-1)x+m2=0的两个实数根分别为x1,x2,且x1+x2>0,x1x2>0,则m的取值范围是( )
A、m≤
| ||
B、m≤
| ||
| C、m<1 | ||
| D、m<1且m≠0 |
考点:根的判别式,根与系数的关系
专题:判别式法
分析:先由根的判别式可得方程有两个实数根则△≥0,根据根与系数的关系得出x1+x2=-2(m-1),x1x2=m2,再由x1+x2>0,x1x2>0,解出不等式组即可.
解答:解:∵△=[2(m-1)]2-4m2=-8m+4≥0,
∴m≤
,
∵x1+x2=-2(m-1)>0,x1x2=m2>0
∴m<1,m≠0
∴m≤
且m≠0.
故选:B.
∴m≤
| 1 |
| 2 |
∵x1+x2=-2(m-1)>0,x1x2=m2>0
∴m<1,m≠0
∴m≤
| 1 |
| 2 |
故选:B.
点评:此题考查了根的判别式和根与系数的关系,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根,根与系数的关系是x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
已知某种植物花粉的直径约为0.00035米,用科学记数法表示是( )
| A、-3.5×104米 |
| B、3.5×10-3米 |
| C、3.5×10-4米 |
| D、3.5×10-5米 |
我国吐鲁番盆地最低点的海拔是-a(a>0)米,死海湖面的海拔更低为-b(b>0)米,则死海湖面的海拔比吐鲁番盆地最低点的海拔低( )米.
| A、a+b | B、-b-a |
| C、-b+a | D、-a+b |
 如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为
如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为 已知二次函数y=a(x-1)2+c的图象如图,则一次函数y=ax+c的大致图象可能是( )
已知二次函数y=a(x-1)2+c的图象如图,则一次函数y=ax+c的大致图象可能是( )




 在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出与△ABC关于y轴对称的图形.
在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出与△ABC关于y轴对称的图形.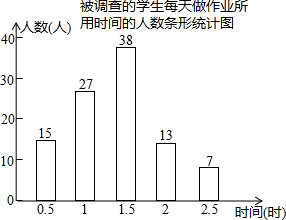 某校学生会为了解本校学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查,在确定调查对象时,大家提出以下几种方案:
某校学生会为了解本校学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查,在确定调查对象时,大家提出以下几种方案: