题目内容
7．
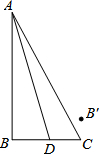如图，已知∠B=90°，AB=3cm，BC=$\sqrt{3}$cm，点D是线段BC上的一个动点，连接AD，动点B′始终与点B关于直线AD对称，当点D由点B位置向右运动至点C位置时，相应的点B′所经过的路程为（ ）| A． | 3cm | B． | πcm | C． | 2$\sqrt{3}$cm | D． | 2πcm |
分析 则点D由点B位置向右运动至点C位置时，相应的点B′所经过的路径是以A为圆心，∠BAC的2倍为圆心角，半径是AB的弧，利用弧长公式即可求解．
解答 解：在直角△ABC中，tan∠BAC=$\frac{BC}{AB}$=$\frac{\sqrt{3}}{3}$，
则∠ABC=30°，
则点D由点B位置向右运动至点C位置时，相应的点B′所经过的路程为：$\frac{60π×3}{180}$=π（cm）．
故选B．
点评 本题考查了点的运动轨迹和弧长公式，以及三角函数，正确理解点B′所经过的路径是以A为圆心，∠BAC的2倍为圆心角，半径是AB的弧是关键．
练习册系列答案
相关题目
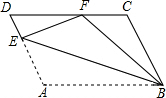如图，在?ABCD中，E为AD上一点，以BE为折痕将△ABE向上翻折，点A恰好落在CD上的点F处．若△FDE的周长为12，△FCB的周长为22，则FC的长为5．
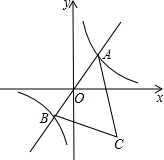如图，已知A是双曲线y=$\frac{7}{x}$在第一象限的分支上一个动点，连接AO并延长另一分支于点B，以AB为一边作等边△ABC，点C在第四象限，随着点A的运动，点C的位置也不断发生变化，但点C始终在双曲线y=$\frac{k}{x}$（k＜0）上运动，则k的值是-21．
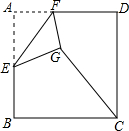如图，在边长为2的正方形ABCD中，E是AB的中点，F是AD边上的一个动点，将△AEF沿EF所在直线折叠得到△GEF，连接GC，则GC长度的最小值是$\sqrt{5}$-1．
如图，王老师在上多边形外角和这节课时，做了一个活动，让小明在操场上从A点出发前进1m，向右转30°，再前进1m，又向右转30°，…，这样一直走下去，直到他第一次回到出发点A为止，他所走的路径构成了一个多边形．小明一共走了12m，这个多边形的内角和是1800度．
将一副三角板按如图放置，则下列结论①∠1=∠3；②如果∠2=30°则有AC∥DE；③如果∠2=30°，则有BC∥AD；④如果∠2=30°，必有∠4=∠C，其中正确的有（ ）