题目内容
11.某中学组织学生去福利院慰问,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.(1)求甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2000元,那么最多可购买多少个甲礼品?
分析 (1)设购买一个乙礼品需要x元,根据“花费600元购买甲礼品和花费360元购买乙礼品的数量相等”列分式方程求解即可;
(2)设总费用不超过2000元,可购买m个甲礼品,则购买乙礼品(30-m)个,根据题意列不等式求解即可.
解答 解:(1)设购买一个乙礼品需要x元,根据题意得:
$\frac{600}{x+40}$=$\frac{360}{x}$,
解得:x=60,
经检验x=60是原方程的根,
∴x+40=100.
答:甲礼品100元,乙礼品60元;
(2)设总费用不超过2000元,可购买m个甲礼品,则购买乙礼品(30-m)个,
根据题意得:100m+60(30-m)≤2000,
解得:m≤5.
答:最多可购买5个甲礼品.
点评 此题主要考查了分式方程和不等式的应用,关键是正确理解题意,找出题目中的等量关系和不等关系,列出方程和不等式.

练习册系列答案
相关题目
2.若x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k≤-1且k≠0 | B. | k<-1且k≠0 | C. | k≥-1且k≠0 | D. | k>-1且k≠0 |
7.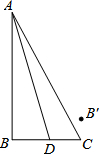 如图,已知∠B=90°,AB=3cm,BC=$\sqrt{3}$cm,点D是线段BC上的一个动点,连接AD,动点B′始终与点B关于直线AD对称,当点D由点B位置向右运动至点C位置时,相应的点B′所经过的路程为( )
如图,已知∠B=90°,AB=3cm,BC=$\sqrt{3}$cm,点D是线段BC上的一个动点,连接AD,动点B′始终与点B关于直线AD对称,当点D由点B位置向右运动至点C位置时,相应的点B′所经过的路程为( )
 如图,已知∠B=90°,AB=3cm,BC=$\sqrt{3}$cm,点D是线段BC上的一个动点,连接AD,动点B′始终与点B关于直线AD对称,当点D由点B位置向右运动至点C位置时,相应的点B′所经过的路程为( )
如图,已知∠B=90°,AB=3cm,BC=$\sqrt{3}$cm,点D是线段BC上的一个动点,连接AD,动点B′始终与点B关于直线AD对称,当点D由点B位置向右运动至点C位置时,相应的点B′所经过的路程为( )| A. | 3cm | B. | πcm | C. | 2$\sqrt{3}$cm | D. | 2πcm |
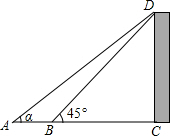 如图,在A处看建筑物CD的顶端D的仰角为α,且tanα=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为7米.
如图,在A处看建筑物CD的顶端D的仰角为α,且tanα=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为7米.