题目内容
 如图,O为AC,BD的中点,则图中全等三角形共有( )对.
如图,O为AC,BD的中点,则图中全等三角形共有( )对.| A、2 | B、3 | C、4 | D、5 |
考点:全等三角形的判定
专题:
分析:平行四边形的性质是:对边相互平行且相等,对角线互相平分.这样不难得出:AD=BC,AB=CD,AO=CO,DO=BO,再利用“对顶角相等”就很容易找到全等的三角形:△ACD≌△CAB(SSS),△ABD≌△CDB(SSS),△AOD≌△COB(SAS),△AOB≌△COD(SAS).
解答:解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC;OD=OB,OA=OC;
在△AOD和△COB中,
,
∴△AOD≌△COB(SAS);①
同理可得出△AOB≌△COD(SAS);②
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS);③
同理可得:△ACD≌△CAB(SSS).④
因此本题共有4对全等三角形.
故选C.
∴AB=CD,AD=BC;OD=OB,OA=OC;
在△AOD和△COB中,
|
∴△AOD≌△COB(SAS);①
同理可得出△AOB≌△COD(SAS);②

在△ABD和△CDB中,
|
∴△ABD≌△CDB(SSS);③
同理可得:△ACD≌△CAB(SSS).④
因此本题共有4对全等三角形.
故选C.
点评:此题考查了平行四边形的性质和全等三角形的判定,三角形全等的条件有时候是直接给的,有时候是根据已知条件推出的,还有时是由已知图形的性质得出的,做题时要全面考虑.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
在△ABC中,∠A=∠B,若与△ABC全等的三角形中有一个角为90°,则△ABC中等于90°的角是( )
| A、∠A | B、∠B |
| C、∠C | D、∠B或∠C |
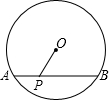 如图,⊙O的直径为10,弦AB的长为8,P为弦AB上不同于A,B的一点.若OP的长为整数,则满足条件的点P有( )
如图,⊙O的直径为10,弦AB的长为8,P为弦AB上不同于A,B的一点.若OP的长为整数,则满足条件的点P有( )| A、2个 | B、3个 | C、4个 | D、5个 |
在一个口袋里装有a个红球,b个白球,c个黄球,则任选1个,不是黄球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法中,不正确的是( )
| A、圆是轴对称图形 |
| B、圆的任意一条直径所在的直线都是圆的对称轴 |
| C、圆的任一直径都是圆的对称轴 |
| D、经过圆心的任意直线都是圆的对称轴 |
式子-□•(3a2b)=12a5b2c成立时,□内应填上( )
| A、4a3bc |
| B、36a3bc |
| C、-4a3bc |
| D、-36a3bc |
已知一个三角形的面积S与底边x的关系是S=x2-2x+6,要使S有最小值,则x的值为( )
| A、1 | B、2 | C、-1 | D、5 |
 如图,已知AD平分∠BAC,要使△ABD≌△ACD,根据“SAS”,需要添加的条件是
如图,已知AD平分∠BAC,要使△ABD≌△ACD,根据“SAS”,需要添加的条件是