题目内容
某商店销售A型和B型两种型号的电脑,销售一台A型电脑可获利120元,销售一台B型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的3倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y与x的关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售利润最大?
(3)若限定商店最多购进A型电脑60台,则这100台电脑的销售总利润能否为13600元?若能,请求出此时该商店购进A型电脑的台数;若不能,请求出这100台电脑销售总利润的范围.
解:(1)由题意可得:y=120x+140(100﹣x)=﹣20x+14000;
(2)据题意得,100﹣x≤3x,解得x≥25,
∵y=﹣20x+14000,﹣20<0,
∴y随x的增大而减小,
∵x为正整数,
∴当x=25时,y取最大值,则100﹣x=75,
即商店购进25台A型电脑和75台B型电脑的销售利润最大;
(3)据题意得,y=(100+m)x+140(100﹣x),即y=(m﹣40)x+14000,
25≤x≤60
①当 0<m<40时,y随x的增大而减小,
0<m<40时,y随x的增大而减小,
∴当x=25时,y取最大值,
即商店购进25台A型电脑和75台B型电脑的销售利润最大.
②m=40时,m﹣40=0,y=14000,
即商店购进A型电脑数量满足25≤x≤60的整数时,均获得最大利润;
③当40<m<100时,m﹣40>0,y随x的增大而增大,
∴当x=60时,y取得最大值.
即商店购进60台A型电脑和40台B型电脑的销售利润最大.

练习册系列答案
相关题目

 +
+ ﹣
﹣ ×(2+
×(2+ )
)
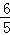 B. 2 C.
B. 2 C. 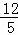 D.
D.