Question

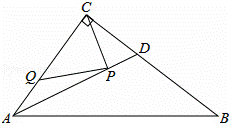
如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，AD是△ABC的角平分线，若P，Q分别是AD和AC边上的动点，则PC+PQ的最小值是（　　）

　 A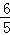．  B． 2 C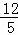．  D．

Answer 1

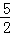
C

考点： 轴对称-最短路线问题． 

分析： 由轴对称的性质可知：PC=PC′，所以QP+PC=QP+PC′，由垂线段最短可知：当C′Q⊥AC时，C′Q有最小值，然后利用锐角三角函数的定义即可其肚饿QC′的长．

解答： 解：如图所示：将△ACD沿AD翻折得到△ADC′，连接DC′，过点C′作C′Q⊥AC．

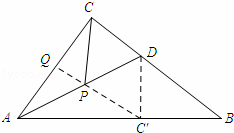
∵AD是∠CAB的角平分线，

∴△ACD与△ADC′关于AD对称．

∴点C′在AB上．

由翻折的性质可知：AC′=AC=3，．PC=PC′．

∴QP+PC=QP+PC′．

由垂线段最短可知：当C′Q⊥AC时，C′Q有最小值．

在Rt△ACB中，AB=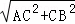==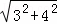5．

∴sin∠CAB=．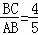

在Rt△AQC′中，sin∠QAC′=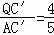，即．

∴QC′=．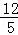

故选：C．

点评： 本题主要考查的是翻折的性质、垂线段最短、勾股定理的应用，锐角三角函数的定义，明确当C′Q⊥AC时，C′Q有最小值是解题的关键．