题目内容
13.点(2m-3,m-2)在第四象限,则m的取值范围是$\frac{3}{2}$<m<2.分析 根据第四象限内点的横坐标大于零,纵坐标小于零,可得不等式组,根据解不等式组,可得答案.
解答 解:由点(2m-3,m-2)在第四象限,得
$\left\{\begin{array}{l}{2m-3>0}\\{m-2<0}\end{array}\right.$,
解得$\frac{3}{2}$<m<2,
故答案为:$\frac{3}{2}$<m<2.
点评 本题考查了点的坐标,利用点的横坐标大于零、纵坐标小于零得出不等式组是解题关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
8.下列语句不正确的是( )
| A. | 直角三角形斜边上的中线等于连结两直角边的中点的中位线 | |
| B. | 对角线相等且垂直的四边形是正方形 | |
| C. | 角平分线上任意一点与每条边上到顶点的距离相等的点的连线段相等 | |
| D. | 顺次连结对角线垂直的四边形各边中点的四边形是矩形 |
2.命题:①对顶角相等;②垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中假命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
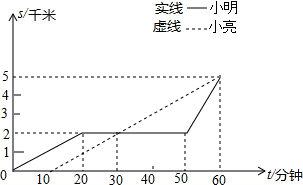 小明与小亮从学校出发到距学校5千米的图书馆看书,下图反应了他们两人离开学校的路程与时间的关系.据图回答以下问题:
小明与小亮从学校出发到距学校5千米的图书馆看书,下图反应了他们两人离开学校的路程与时间的关系.据图回答以下问题: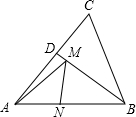 如图,在锐角三角形ABC中,AB=2,∠ABC=60°,∠ABC的平分线交AC于D,M、N分别是BD、AB上的动点,则AM+MN的最小值是$\sqrt{3}$.
如图,在锐角三角形ABC中,AB=2,∠ABC=60°,∠ABC的平分线交AC于D,M、N分别是BD、AB上的动点,则AM+MN的最小值是$\sqrt{3}$.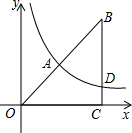 如图,平面直角坐标系中,点B在第一象限,OC=BC,∠OCB=90°,OB=4$\sqrt{2}$,且反比例函数y=$\frac{m}{x}$(m≠0)的图象经过OB的中点A.
如图,平面直角坐标系中,点B在第一象限,OC=BC,∠OCB=90°,OB=4$\sqrt{2}$,且反比例函数y=$\frac{m}{x}$(m≠0)的图象经过OB的中点A.