题目内容
4．已知抛物线y=a（x-2）2+k（a＞0，a，k常数），A（-3，y1）B（3，y2）C（4，y3）是抛物线上三点，则y1，y2，y3用“＜”排列为y2＜y3＜y1．分析 先根据顶点式得到抛物线y=a（x-2）2+k（a＞0，a，k为常数）的对称轴为直线x=2，然后二次函数的性质和A点、B点和C点离对称轴的远近进行判断．
解答 解：抛物线y=a（x-2）2+k（a＞0，a，k为常数）的对称轴为直线x=2，
因为|-3-2|＞|4-2|＞|3-2|．
所以A（-3，y1）到直线x=2的距离为5，B（3，y2）到直线x=2的距离为1，C（4，y3）到直线的距离为2，
所以y2＜y3＜y1．
故答案为y2＜y3＜y1．
点评 本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了二次函数的性质．
练习册系列答案
相关题目
已知：如图，直线AB和CD相交于点O，射线OE⊥AB于点O，射线OF⊥CD于点O，且∠BOF=35°，求∠AOC和∠DOE的度数．
如图，将一个边长为1的正方形纸片分割成6部分，部分①是整体面积的一半，部分②是部分①面积的一半，部分③是部分②面积的一半，依此类推．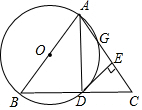
如图，以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D，交AC于点G，连结AD，并过点D作⊙O的切线DE，交AC于点E．求证：