题目内容
9.若a是正整数,且a满足$\left\{\begin{array}{l}{1-2a<-1}\\{\frac{3-a}{2}>0}\end{array}\right.$,试解分式方程$\frac{3}{ax-a}$+$\frac{x}{x+1}$=1.分析 求出已知不等式组的解集确定出a的范围,进而确定出正整数a的值,代入分式方程计算即可求出解.
解答 解:不等式组$\left\{\begin{array}{l}{1-2a<-1①}\\{\frac{3-a}{2}>0②}\end{array}\right.$,
由①得:a>1;
由②得:a<3,
∴不等式组的解集为1<a<3,
∵a是正整数,
∴a=2,
将a=2代入分式方程得$\frac{3}{2x-2}$+$\frac{x}{x+1}$=1,
去分母,方程两边同时乘以2(x+1)(x-1)得:3x+3-2x2-2x=2x2-2,
解得:x=-5,
经检验,原分式方程的解是x=-5.
点评 此题考查了解分式方程,以及一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
19.某小区开展“节约用水,从我做起”活动,下表是从该小区抽取的10个家庭与上月比较的一个月的节水情况统计:
那么这10个家庭的节水量(m3)的平均数和中位数分别是( )
| 节水量(m3) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| 家庭数(个) | 1 | 2 | 2 | 4 | 1 |
| A. | 0.42和0.4 | B. | 0.4和0.4 | C. | 0.42和0.45 | D. | 0.4和0.45 |
20.一元二次方程x2-x-2=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
17.下列命题中是假命题的是( )
| A. | 一个三角形中至少有两个锐角 | |
| B. | 在同一平面内,垂直于同一直线的两条直线平行 | |
| C. | 同角的补角相等 | |
| D. | 如果a为实数,那么|a|>0 |
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. | 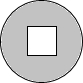 |