题目内容
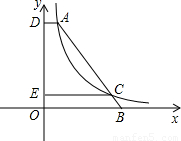 如图,A为双曲线y=
如图,A为双曲线y=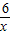 上一点,AD⊥y轴于点D,将直线AD向下平移交双曲线于C,交y轴于E,延长AC交x轴于点B,
上一点,AD⊥y轴于点D,将直线AD向下平移交双曲线于C,交y轴于E,延长AC交x轴于点B,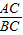 =2,则
=2,则 = .
= .
【答案】分析:设E的纵坐标是a,则D的纵坐标是3a,则A的纵坐标是3a,则AD,CE可以利用a表示出来,然后根据相似三角形的对应边的毕相等,即可求得BN的长,即可得到OB的长,然后代入式子化简即可求解.
解答: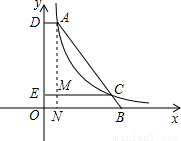 解:作AN⊥y轴,交CE与M.则AD=EM=ON.
解:作AN⊥y轴,交CE与M.则AD=EM=ON.
∵AD∥CE∥y轴,
∴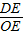 =
=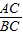 =2,
=2,
设E的纵坐标是a,则D的纵坐标是3a,A的纵坐标是3a,C的纵坐标是a.
把y=3a代入函数y=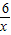 得到:y=
得到:y=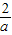 ,则AD=
,则AD=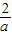 ;
;
把y=a代入函数y=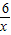 得到:y=
得到:y=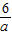 ,则CE=
,则CE=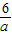 .
.
则CM=CE-EM=CE-AD=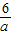 -
-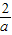 =
=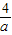 .
.
∵CE∥y轴,
∴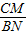 =
=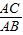 =
= ,
,
∴BN= CM=
CM=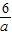 ,
,
∴OB=BN+ON=BN+AD=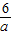 +
+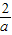 =
=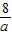 .
.
则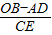 =
=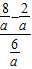 =1.
=1.
故答案是:1.
点评:本题考查了反比例函数与相似三角形的性质的综合应用,正确表示出BN的长度是关键.
解答:
 解:作AN⊥y轴,交CE与M.则AD=EM=ON.
解:作AN⊥y轴,交CE与M.则AD=EM=ON.∵AD∥CE∥y轴,
∴
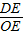 =
=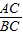 =2,
=2,设E的纵坐标是a,则D的纵坐标是3a,A的纵坐标是3a,C的纵坐标是a.
把y=3a代入函数y=
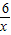 得到:y=
得到:y=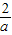 ,则AD=
,则AD=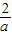 ;
;把y=a代入函数y=
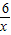 得到:y=
得到:y=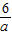 ,则CE=
,则CE=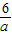 .
.则CM=CE-EM=CE-AD=
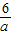 -
-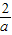 =
=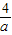 .
.∵CE∥y轴,
∴
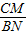 =
=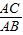 =
= ,
,∴BN=
 CM=
CM=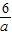 ,
,∴OB=BN+ON=BN+AD=
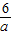 +
+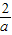 =
=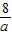 .
.则
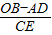 =
=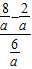 =1.
=1.故答案是:1.
点评:本题考查了反比例函数与相似三角形的性质的综合应用,正确表示出BN的长度是关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 (2012•兰州)如图,M为双曲线y=
(2012•兰州)如图,M为双曲线y= (2013•历城区二模)如图,M为双曲线
(2013•历城区二模)如图,M为双曲线 如图,A为双曲线y=
如图,A为双曲线y= (2013•天门模拟)如图,B为双曲线y=
(2013•天门模拟)如图,B为双曲线y= 如图,C为双曲线y=
如图,C为双曲线y=