Question

【题目】如图，在中，，，以为一边向上作等边三角形，点在垂直平分线上，且，连接，，.

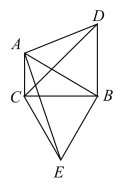
（1）判断的形状，并说明理由；

（2）求证：；

（3）填空：

①若，相交于点，则的度数为______.

②在射线上有一动点，若为等腰三角形，则的度数为______.

Answer 1

【答案】（1）△CBE是等边三角形 理由见解析；（2）见解析；（3）① 60，② 15或60或105

【解析】

（1）由垂直平分线的性质可得EC=EB，再算出∠CBE=60°，可判定；

（2）通过证明△ABE≌△DBC可得；

（3）①由（2）中全等可得∠EAB=∠CDB，再根据三角形内角和可得∠AFD的度数；

②分PB=PB，BP=BC，CP=CB三种情况讨论，通过等腰三角形的性质，借助∠ABC的度数计算∠ACP的度数.

解：（1）△CBE是等边三角形 理由如下：

∵点E在BC垂直平分线上

∴EC＝EB

∵EB⊥AB

∴∠ABE＝90

∵∠ABC＝30

∴∠CBE＝60

∴△CBE是等边三角形

（2）∵△ABD是等边三角形

∴AB＝DB，∠ABD＝60

∵∠ABC＝30

∴∠DBC＝90

∵EB⊥AB

∴∠ABE＝90

∴∠ABE＝∠DBC

由（1）可知：△CBE是等边三角形

∴EB＝CB

∴△ABE≌△DBC（SAS）

∴AE＝DC

（3）①设AB与CD交于点G，

∵△ABE≌△DBC

∴∠EAB=∠CDB，

又∵∠AGC=∠BGD

∴∠AFD=∠ABD=60°.

② ∵△BCP为等腰三角形，如图，

当BC=BP时，

∠ABC=∠BCP+∠BPC=30°，

∴∠BCP=15°，

∴∠ACP=90°+15°=105°；

当PC=PB时，

∵∠ABC=30°，

∴∠PCB=30°，

∵∠ACB=90°，

∴∠ACP=60°；

当BP=BC时，

∵∠ABC=30°，

∴∠PCB=∠CPB=（180°-30°）=75°，

∴∠ACP=90°-75°=15°.

综上：∠ACP的度数为15或60或105.