题目内容
有理数a、b、c在数轴上对应的位置如图所示,

化简:|a+c|-|a-b-c|+|b-a|-|b-c|.

化简:|a+c|-|a-b-c|+|b-a|-|b-c|.
考点:整式的加减,数轴,绝对值
专题:
分析:先根据各点在数轴上的位置判断出其符号,再去绝对值符号,合并同类项即可.
解答:解:∵由图可知,c<-1<b<a,
∴a+c>0,a-b-c>0,b-a<0,b-c>0,
∴原式=a+c-(a-b-c)-(b-a)-(b-c)
=a+c-a+b+c-b+a-b+c
=a-b+c.
∴a+c>0,a-b-c>0,b-a<0,b-c>0,
∴原式=a+c-(a-b-c)-(b-a)-(b-c)
=a+c-a+b+c-b+a-b+c
=a-b+c.
点评:本题考查的是整式的加减,熟知整式的加减实质上就是合并同类项是解答此题的关键.

练习册系列答案
相关题目
下列代数式的值中,一定是负数的是( )
| A、-(x+1)2 |
| B、-|x+1|+2 |
| C、(-x)2 |
| D、-x2-1 |
 如图,AC=AD,BA=BD,则有( )
如图,AC=AD,BA=BD,则有( )| A、AB垂直平分CD |
| B、CD垂直平分AB |
| C、AB与CD互相垂直平分 |
| D、CD平分∠ACB |
把一个正方形纸片折叠三次后沿虚线剪断①②两部分,则展开①后得到的是( )


A、 |
B、 |
C、 |
D、 |
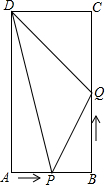 如图,在矩形ABCD中,AB=6cm.BC=12cm,点P从点A沿边向点B以1cm/s的速度移动;同时,点Q从点B沿边向点C以2cm/s的速度移动.
如图,在矩形ABCD中,AB=6cm.BC=12cm,点P从点A沿边向点B以1cm/s的速度移动;同时,点Q从点B沿边向点C以2cm/s的速度移动. 已知a,b,c均为有理数,在数轴上对应点的位置如图所示,则|a+c|-|b-a|+|b+c|=
已知a,b,c均为有理数,在数轴上对应点的位置如图所示,则|a+c|-|b-a|+|b+c|=