题目内容
16.已知x1,x2是一元二次方程4kx2-4kx+k+2=0的两个实数根.是否存在实数k,使(2x1-x2)(x1-2x2)=-$\frac{3}{2}$成立?若存在,求出k的值;若不存在,请您说明理由.分析 先利用一元二次方程的定义和根的判别式得到4k≠0,且△=(-4k)2-4k(k+2)≥0,解得k<0,再利用根与系数的关系得到x1+x2=1,x1x2=$\frac{k+2}{4k}$,则利用(2x1-x2)(x1-2x2)=-$\frac{3}{2}$得到2(x1+x2)2-9(x1x2)=-$\frac{3}{2}$,所以2×12-9•$\frac{k+2}{4k}$=-$\frac{3}{2}$,解得k=$\frac{18}{5}$,然后利用k<0可判定不存在k的值.
解答 解:不存在.
理由如下:
根据题意得4k≠0,且△=(-4k)2-4k(k+2)≥0,
∴k<0,
∵x1,x2是一元二次方程4kx2-4kx+k+2=0的两个实数根,
∴x1+x2=1,x1x2=$\frac{k+2}{4k}$,
∵(2x1-x2)(x1-2x2)=-$\frac{3}{2}$,
∴2(x1+x2)2-9(x1x2)=-$\frac{3}{2}$,
∴2×12-9•$\frac{k+2}{4k}$=-$\frac{3}{2}$,解得k=$\frac{18}{5}$,
而k<0,
∴不存在k的值,使(2x1-x2)(x1-2x2)=-$\frac{3}{2}$成立.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
18.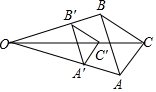 如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )
如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )
 如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )
如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )| A. | 2:3 | B. | 3:2 | C. | 4:5 | D. | 4:9 |
8.下列说法中,正确的是( )
| A. | 同位角相等 | B. | 矩形的对角线一定互相垂直 | ||
| C. | 对角线相等的四边形是矩形 | D. | 四条边相等的四边形是菱形 |
 已知,(如图)AD⊥BC垂足为D,EF⊥BC垂足为F,若∠1=∠2,问GD与AC平行吗?为什么?
已知,(如图)AD⊥BC垂足为D,EF⊥BC垂足为F,若∠1=∠2,问GD与AC平行吗?为什么?