题目内容
18.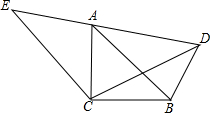 已知:如图△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上.请证明:
已知:如图△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上.请证明:(1)△CBD≌△CAE;
(2)∠ADB=90°.
分析 (1)根据等腰直角三角形的性质得到∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,AC2+BC2=AB2,于是得到2AC2=AB2,∠ECD-∠ACD=∠ACB-∠ACD,求得∠ACE=∠BCD.根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到AE=BD,∠E=∠BDC.求得∠BDC=45°,于是得到∠BDC+∠ADC=90°,即可得到结论.
解答 证明:(1)∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,
EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2,∠ECD-∠ACD=∠ACB-∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{EC=DC}\end{array}\right.$,
∴△CBD≌△CAE;
(2)∵△CBD≌△CAE,
∴AE=BD,∠E=∠BDC.
∴∠BDC=45°,
∴∠BDC+∠ADC=90°,
即∠ADB=90°.
点评 本题考查了等腰直角三角形的性质的运用,直角三角形的判定及性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.两种移动电话计费式表:
(1)根据题意,一个月内在本地通话时间如下,请填下表
(2)当通话时间是多少时,使用两种移动电话费用一样?
(3)什么情况下,使用神州行?什么情况下,使用全球通?
| 全球通 | 神州行 | |
| 月租费 | 50元/月 | 0 |
| 本地通话费 | 0.40元/分 | 0.60元/分 |
| 时间(分) | 80 | 120 | x |
| 全球通费用 | 82 | 98 | 50+0.4x |
| 神州行费用 | 48 | 72 | 0.6x |
(3)什么情况下,使用神州行?什么情况下,使用全球通?
10.小强买了张50元的乘车IC卡,如果他乘车的次数用m表示,则记录他每次乘车后的余额n(元)如下表:
(1)写出乘车的次数m表示余额n的关系式.
(2)利用上述关系式计算小强乘了10次车还剩下多少元?
(3)小强最多能乘几次车?
| 次数 m | 余额 n(元) |
| 1 | 50-0.9 |
| 2 | 50-1.8 |
| 3 | 50-2.7 |
| 4 | 50-3.6 |
| … | … |
(2)利用上述关系式计算小强乘了10次车还剩下多少元?
(3)小强最多能乘几次车?
 如图,反向延长OA得射线OE.
如图,反向延长OA得射线OE.