题目内容
13.(1)在△ABC中,∠A-∠B=90°.试判定△ABC的形状;(2)在△ABC中,AC=5,中线AD=7,求AB边的取值范围.
分析 (1)由∠A-∠B=90°,可得∠A>90°,再根据三角形内角和定理可证出∠A<180°,进而可得三角形是钝角三角形.
(2)延长AD到E,使DE=AD,然后利用“边角边”证明△ABD和△ECD全等,根据全等三角形对应边相等可得CE=AB,然后根据三角形任意两边之和大于第三边,两边之差小于第三边求出AE的取值范围,然后即可得解.
解答 解:(1)△ABC为钝角三角形,
∵∠A-∠B=90°,
∴∠A>90°,
∵∠A+∠B+∠C=180°,
∴∠A<180°,
∴90°<∠A<180°,
∴△ABC是钝角三角形;
(2)如图,延长AD至E,是DE=AD,连接CE,
∵AD是△ABC的中线,
∴BD=CD,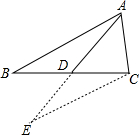
在△ABD和△ECD中,
$\left\{\begin{array}{l}{AD=DE}\\{∠ADE=∠EDC}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ECD(SAS),
∴AB=CE,DE=AD=7,
∵AC=5,
∴14-5<EC<14+5,
∴9<EC<19.
∴9<AB<19,
故答案为:9<AB<19.
点评 此题主要考查了三角形的内角,三角形的三边关系、全等三角形的判定与性质,遇中点加倍延,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
 实数a、b在数轴上的位置如图所示,化简|a|+|b|-|a+b|.
实数a、b在数轴上的位置如图所示,化简|a|+|b|-|a+b|. 某型号的飞机的机翼形状如图所示,其中AB∥CD,请你根据图中的数据计算AC、BD和CD的长度(单位:米.结果保留根号).
某型号的飞机的机翼形状如图所示,其中AB∥CD,请你根据图中的数据计算AC、BD和CD的长度(单位:米.结果保留根号). 已知:如图△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上.请证明:
已知:如图△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上.请证明: