题目内容
1.用长度相等的小火柴棒摆出下列一组图形(图中最小正方形的边长即为一根火柴棒的长)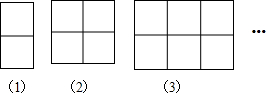
(1)填写下表:
| 图形编号 | (1) | (2) | (3) | (4) |
| 图形中火柴棒的根数 | 7 | 12 | 17 | 22 |
(3)小丽说“照这样的方式摆下去,总会有相邻两个图形所用火柴棒的总数恰好等于2015”.你同意他的说法吗?为什么吗?
分析 (1)(2)由题意可知:摆第(1)个图形火柴棒2×2+1×3=7根,摆第(2)个图形火柴棒2×3+2×3=12根,摆第(3)个图形火柴棒2×4+3×3=12根,摆第(4)个图形火柴棒2×5+4×3=12根,…由此得出摆第(n)个图形火柴棒2(n+1)+3n=(5n+2)根;
(3)由(2)中的规律得出相邻两个图形所用火柴棒的总数,建立方程求得方程的解,进一步判定即可.
解答 解:(1)填表如下:
| 图形编号 | (1) | (2) | (3) | (4) |
| 图形中火柴棒的根数 | 7 | 12 | 17 | 22 |
(3)不同意.
理由如下:
假设存在满足题意的整数n,则有:
5n+2+5(n+1)+2=2015,
解得:n=$\frac{1003}{5}$,
此时n非整数,所以不存在这样的n.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
9.当x-y=-3时,代数式-4-x+y的值等于( )
| A. | -1 | B. | 7 | C. | -7 | D. | 1 |
16.代数式-3x,0,2x-y,$\frac{2x+y}{4}$,$\frac{3b}{a}$中,单项式的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.$\sqrt{m-n}$的一个有理化因式是( )
| A. | $\sqrt{m+n}$ | B. | $\sqrt{m-n}$ | C. | $\sqrt{m}$+$\sqrt{n}$ | D. | $\sqrt{m}$-$\sqrt{n}$ |
 如图,已知l1∥l2,∠A=40°,∠1=60°,则∠2的度数为80°.
如图,已知l1∥l2,∠A=40°,∠1=60°,则∠2的度数为80°. 如图,点B在线段AC上,点N为线段AB的中点.点M为线段AC的中点.
如图,点B在线段AC上,点N为线段AB的中点.点M为线段AC的中点.