题目内容
11. 如图,点B在线段AC上,点N为线段AB的中点.点M为线段AC的中点.
如图,点B在线段AC上,点N为线段AB的中点.点M为线段AC的中点.(1)若MN=5cm,求线段BC的长度;
(2)若BC=10cm,求线段MN的长度.
分析 (1)根据线段中点的性质得到AN=$\frac{1}{2}$AB,AM=$\frac{1}{2}$AC,得到MN=$\frac{1}{2}$BC,计算即可;
(2)根据MN=$\frac{1}{2}$BC计算即可得到答案.
解答 解:(1)∵点N为线段AB的中点,
∴AN=$\frac{1}{2}$AB,
∵点M为线段AC的中点,
∴AM=$\frac{1}{2}$AC,
∴MN=AM-AN=$\frac{1}{2}$(AC-AB)=$\frac{1}{2}$BC,
∵MN=5cm,
∴BC=10cm;
(2)由(1)得,MN=$\frac{1}{2}$BC=5cm.
点评 本题考查的是两点间的距离,正确理解线段中点的意义是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
1.用长度相等的小火柴棒摆出下列一组图形(图中最小正方形的边长即为一根火柴棒的长)
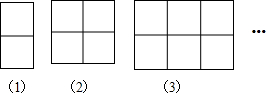
(1)填写下表:
(2)照这样的方式摆下去,写出摆第(n)个图形火柴棒的根数(用含n的代数式表示,直接写出答案);
(3)小丽说“照这样的方式摆下去,总会有相邻两个图形所用火柴棒的总数恰好等于2015”.你同意他的说法吗?为什么吗?

(1)填写下表:
| 图形编号 | (1) | (2) | (3) | (4) |
| 图形中火柴棒的根数 | 7 | 12 | 17 | 22 |
(3)小丽说“照这样的方式摆下去,总会有相邻两个图形所用火柴棒的总数恰好等于2015”.你同意他的说法吗?为什么吗?
2.一只蚂蚁从数轴上A点出发爬了6个单位长度到了表示1的点,则点A所表示的数是( )
| A. | 7 | B. | -5 | C. | 7或-5 | D. | 5或-7 |
16. 如图所示,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中等腰三角形有( )
如图所示,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中等腰三角形有( )
 如图所示,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中等腰三角形有( )
如图所示,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中等腰三角形有( )| A. | 3个 | B. | 5个 | C. | 7个 | D. | 8个 |
 如图,已知∠A,求作∠B=$\frac{1}{4}$∠A.(不写作法,保留作图痕迹)
如图,已知∠A,求作∠B=$\frac{1}{4}$∠A.(不写作法,保留作图痕迹)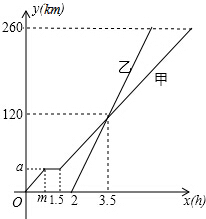 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.请根据图象提供的信息解答下列各题:
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.请根据图象提供的信息解答下列各题:
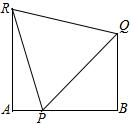 设在一条小巷内,∠A=∠B=90°,一个梯子的底脚位于点P处,当该梯子顶端靠在小巷一侧的墙上点Q时,梯子的倾斜角为45°,当顶端靠在小巷的另一侧墙上时,其顶端R离开地面高度为4米,且此时梯子的倾斜角为75°.
设在一条小巷内,∠A=∠B=90°,一个梯子的底脚位于点P处,当该梯子顶端靠在小巷一侧的墙上点Q时,梯子的倾斜角为45°,当顶端靠在小巷的另一侧墙上时,其顶端R离开地面高度为4米,且此时梯子的倾斜角为75°.