题目内容
3．
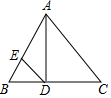如图，在△ABC中，已知AD⊥BC，∠B=64°，DE平分∠ADB，求∠BAD和∠AED的度数．
分析 在Rt△BAD中，根据直角三角形的两个锐角互余的性质可求∠BAD的度数；由DE平分∠ADB，AD⊥BC求得∠BDE=45°，再根据外角定理求解即可．
解答 解：∵AD⊥BC，
∴在Rt△BAD中，∠BAD+∠B=90°，
又∵∠B=64°，
∴∠BAD=26°；
∵AD⊥BC，DE平分∠ADB，
∴∠BDE=45°，
在△BED中，∠B=64°，
∴∠B+∠BDE=109°，
∵∠AED=∠B+∠BDE，
∴∠AED=109°．
点评 此题考查了直角三角形的两个锐角互余的性质，同时考查了角平分线的定义以及三角形外角的性质．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
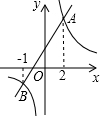如图，一次函数y=kx+b（k、b为常数，且k≠0）的图象与反比例函数y=$\frac{m}{x}$（m为常数，且m≠0）的图象交于A、B两点．则关于x的方程kx+b=$\frac{m}{x}$的解为-1和2．
已知，如图，∠BAG=45°，∠AGD=135°，∠E=∠F．求证：∠BAE=∠CGF．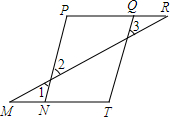
如图所示，M、N、T和P、Q、R分别在同一直线上，且∠1=∠3，∠P=∠T．请问∠M=∠R吗？为什么？
