题目内容
5. 如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )
如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )| A. | $\frac{12}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{24}{5}$ | D. | 不确定 |
分析 首先连接OP,由矩形的两条边AB、BC的长分别为3和4,可求得OA=OD=2.5,△AOD的面积,然后由S△AOD=S△AOP+S△DOP=$\frac{1}{2}$OA•PE+OD•PF求得答案.
解答 解:连接OP,
∵矩形的两条边AB、BC的长分别为和4,
∴S矩形ABCD=AB•BC=12,OA=OC,OB=OD,AC=BD=5,
∴OA=OD=2.5,
∴S△ACD=$\frac{1}{2}$S矩形ABCD=6,
∴S△AOD=$\frac{1}{2}$S△ACD=3,
∵S△AOD=S△AOP+S△DOP=$\frac{1}{2}$OA•PE+$\frac{1}{2}$OD•PF=$\frac{1}{2}$×2.5×PE+$\frac{1}{2}$×2.5×PF=$\frac{5}{4}$(PE+PF)=3,
解得:PE+PF=$\frac{12}{5}$.
故选A.
点评 此题考查了矩形的性质以及三角形面积问题.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
7.下列计算正确的是( )
| A. | x3•x4=x12 | B. | 4x4÷2x2=2x2 | C. | |a|=a | D. | (-xy2)3=x3y6 |
5.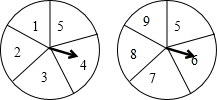 如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
 如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )| A. | $\frac{2}{25}$ | B. | $\frac{4}{25}$ | C. | $\frac{6}{25}$ | D. | $\frac{9}{25}$ |
14.已知x2-y2=4,x-y=2,则x+y等于( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
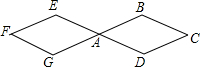 如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行.当电子甲虫爬行2015cm时停下,则它停的位置是( )