题目内容
 如图,有一拱桥呈圆弧形,它的跨度(所对弦长AB)为60m,拱高18m,当水面涨至其跨度只有30m时,就要采取紧急措施.某次洪水来到时,拱顶离水面只有4m,问:是否要采取紧急措施?并说明理由.
如图,有一拱桥呈圆弧形,它的跨度(所对弦长AB)为60m,拱高18m,当水面涨至其跨度只有30m时,就要采取紧急措施.某次洪水来到时,拱顶离水面只有4m,问:是否要采取紧急措施?并说明理由.考点:垂径定理的应用,勾股定理
专题:应用题
分析:连接OA′,OA.设圆的半径是R,则ON=R-4,OM=R-18.根据垂径定理求得AM的长,在Rt△AOM中,根据勾股定理求得R的值,在Rt△A′ON中,根据勾股定理求得A′N的值,再根据垂径定理求得A′B′的长,从而作出判断.
解答: 解:连接OA′,OA.
解:连接OA′,OA.
设圆的半径是R米,则ON=(R-4)米,OM=(R-18)米.
根据垂径定理,得AM=
AB=30米,
在Rt△AOM中,AO2=OM2+AM2,
即R2=(R-18)2+900,
解得:R=34.
在Rt△A′ON中,根据勾股定理得A′N=
=16米,
根据垂径定理,得:A′B′=2A′N=32>30.
∴不用采取紧急措施.
 解:连接OA′,OA.
解:连接OA′,OA.设圆的半径是R米,则ON=(R-4)米,OM=(R-18)米.
根据垂径定理,得AM=
| 1 |
| 2 |
在Rt△AOM中,AO2=OM2+AM2,
即R2=(R-18)2+900,
解得:R=34.
在Rt△A′ON中,根据勾股定理得A′N=
| 342-302 |
根据垂径定理,得:A′B′=2A′N=32>30.
∴不用采取紧急措施.
点评:本题考查了垂径定理在实际问题中的运用,另外,求是否采取紧急措施要转换为A'B'的长度是否大于30m.

练习册系列答案
相关题目
 如图,AB=DC,BF=CE,AE=DF,你能找到一对全等的三角形吗?说明理由.
如图,AB=DC,BF=CE,AE=DF,你能找到一对全等的三角形吗?说明理由. 如图(1、2)的直线a与b既不相交也不平行,为什么会出现这样的情况?与同学们讨论一下.
如图(1、2)的直线a与b既不相交也不平行,为什么会出现这样的情况?与同学们讨论一下.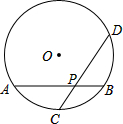 如图,在一直径为8m的圆形戏水池中搭有两座浮桥AB,CD,已知C是
如图,在一直径为8m的圆形戏水池中搭有两座浮桥AB,CD,已知C是
 如图,若∠ACB=90°,CD⊥AB于点D,则AC边上的高是
如图,若∠ACB=90°,CD⊥AB于点D,则AC边上的高是