题目内容
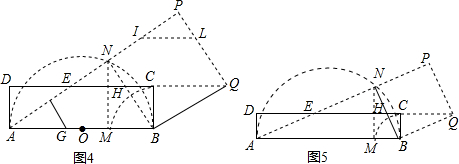
13. 如图,四边形MNPQ中NP∥AQ,NP=2,AN=3,∠Q=60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在四边形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动,求正方形在整个翻滚过程中点A所经过的路线与四边形MNPQ的三边MN、NP、PQ所围成图形的面积S=$\frac{7}{3}$π+2.
如图,四边形MNPQ中NP∥AQ,NP=2,AN=3,∠Q=60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在四边形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动,求正方形在整个翻滚过程中点A所经过的路线与四边形MNPQ的三边MN、NP、PQ所围成图形的面积S=$\frac{7}{3}$π+2.
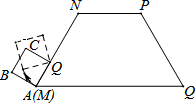
分析 先根据点A绕点D翻滚,然后绕点C翻滚,然后绕点B翻滚,半径分别为1、2、1,翻转角分别为90°、90°、150°,据此画出图形.再结合总结的翻转角度和翻转半径,求出圆弧与梯形的边长围成的扇形的面积即可.
解答  解:如图:
解:如图:
∵点A绕点D翻滚,然后绕点C翻滚,然后绕点B翻滚,半径分别为1、$\sqrt{2}$、1,翻转角分别为90°、90°、150°,
∴S=2×$\frac{90×1×π}{360}$+2×$\frac{90π×(\sqrt{2})^{2}}{360}$+2×$\frac{150π×1}{360}$+4×$\frac{1}{2}$×12
=$\frac{π}{2}$+π+$\frac{5}{6}$π+2
=$\frac{7}{3}$π+2.
故答案为:$\frac{7}{3}$π+2.
点评 本题考查了扇形面积的计算、等腰梯形的性质、旋转的性质,作出图形并熟悉扇形面积是解题的关键.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 两点之间的距离是两点间的线段 | |
| B. | 同一平面内,过一点有且只有一条直线与已知直线平行 | |
| C. | 与同一条直线垂直的两条直线也垂直 | |
| D. | 同一平面内,过一点有且只有一条直线与已知直线垂直 |
2.下列各数等于3的是( )
| A. | -$\sqrt{{3}^{2}}$ | B. | -$\sqrt{(-3)^{2}}$ | C. | (-$\sqrt{\frac{1}{3}}$)2 | D. | $\sqrt{(-\frac{1}{3})^{-2}}$ |
 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为6,则GE+FH的最大值为9.
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为6,则GE+FH的最大值为9. 如图,在平行四边形ABCD中,AB=5,BC=12,对角线交于点O,∠BAD的平分线交BC于E、交BD于F,分别过顶点B、D作AE的垂线,垂足为G、H,连接OG、OH.
如图,在平行四边形ABCD中,AB=5,BC=12,对角线交于点O,∠BAD的平分线交BC于E、交BD于F,分别过顶点B、D作AE的垂线,垂足为G、H,连接OG、OH.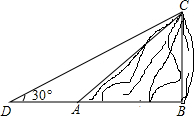 如图,某人在D处测得山顶C的仰角为30°,向前走30米到达山脚A处,测得山坡AC的坡度为i=1:1.5,求山顶的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).
如图,某人在D处测得山顶C的仰角为30°,向前走30米到达山脚A处,测得山坡AC的坡度为i=1:1.5,求山顶的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).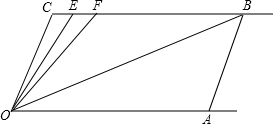 如图,已知直线CB∥OA,∠C=100°,点E、F在CB边上,且满足∠FOB=∠AOB,OE平分∠COF.
如图,已知直线CB∥OA,∠C=100°,点E、F在CB边上,且满足∠FOB=∠AOB,OE平分∠COF.