题目内容
11. 如图,在Rt△ABC中,∠C=90°,AC=5,∠A=30°,求∠B与BC.
如图,在Rt△ABC中,∠C=90°,AC=5,∠A=30°,求∠B与BC.
分析 利用直角三角形两锐角互余求出∠B,根据tanA=$\frac{BC}{AC}$得出BC=AC•tanA,将数值代入计算即可.
解答 解:∵在Rt△ABC中,∠C=90°,AC=5,∠A=30°,
∴∠B=90°-∠A=60°,tanA=$\frac{BC}{AC}$,
∴BC=AC•tanA=5×$\frac{\sqrt{3}}{3}$=$\frac{5\sqrt{3}}{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解直角三角形要用到的关系(在Rt△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边):
①两锐角之间的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:sinA=∠A的对边:斜边=a:c,cosA=∠A的邻边:斜边=b:c,tanA=∠A的对边:∠A的邻边=a:b.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
1.某农科院在相同条件下做了某种玉米种子发芽率的试验,结果如下:
则该玉米种子发芽的概率估计值为0.9(结果精确到0.1).
| 种子总数 | 100 | 400 | 800 | 1000 | 3500 | 7000 | 9000 | 14000 |
| 发芽种子数 | 91 | 354 | 716 | 901 | 3164 | 5613 | 8094 | 12614 |
| 发芽的频率 | 0.91 | 0.885 | 0.895 | 0.901 | 0.904 | 0.902 | 0.899 | 0.901 |
19.一个八边形至少可以分割成三角形的个数为( )
| A. | 8 | B. | 5 | C. | 6 | D. | 7 |
20.下列的数是负数的是( )
| A. | 7 | B. | -6的相反数 | C. | -8 | D. | 以上都不正确 |
 已知线段AB=4cm,延长AB到点C,使BC=$\frac{1}{2}$AB,如果点M为AC的中点,求AM的长度.
已知线段AB=4cm,延长AB到点C,使BC=$\frac{1}{2}$AB,如果点M为AC的中点,求AM的长度.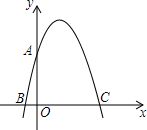 如图,在平面直角坐标系中,点0为坐标原点,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B、C(点B在点C左侧),且OA=OC=4OB.
如图,在平面直角坐标系中,点0为坐标原点,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B、C(点B在点C左侧),且OA=OC=4OB. 如图,已知大长方形ACFH的面积为572,被分割成六个小正方形,设最小的正方形边长a,第二小的正方形边长为b.
如图,已知大长方形ACFH的面积为572,被分割成六个小正方形,设最小的正方形边长a,第二小的正方形边长为b.