题目内容
9.已知两个正比例函数y1=k1x与y2=k2x,当x=2时,y1+y2=-1;当x=3时,y1-y2=12.(1)求这两个正比例函数的解析式;
(2)当x=4时,求$\frac{1}{y_1}+\frac{1}{y_2}$的值.
分析 (1)利用题意列方程组$\left\{\begin{array}{l}{2{k}_{1}+2{k}_{2}=-1}\\{3{k}_{1}-3{k}_{2}=12}\end{array}\right.$,然后解方程组求出k1与k2的值,从而得到两个正比例函数的解析式;
(2)先计算出自变量为4时所对应的两个函数值,然后计算$\frac{1}{y_1}+\frac{1}{y_2}$的值.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{2{k}_{1}+2{k}_{2}=-1}\\{3{k}_{1}-3{k}_{2}=12}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=\frac{7}{4}}\\{{k}_{2}=-\frac{9}{4}}\end{array}\right.$,
所以两正比例函数的解析式分别为y1=$\frac{7}{4}$x,y2=-$\frac{9}{4}$x;
(2)当x=4时,y1=$\frac{7}{4}$x=7,y2=-$\frac{9}{4}$x=-9,
所以$\frac{1}{y_1}+\frac{1}{y_2}$=$\frac{1}{7}$-$\frac{1}{9}$=$\frac{2}{63}$.
点评 本题考查了待定系数法求正比例函数的解析式.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
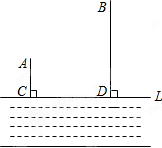 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米.
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米. 如图,在⊙O中,直径AB=10,弦CD⊥AB,垂足为E,BE=2,求弦CD的长.
如图,在⊙O中,直径AB=10,弦CD⊥AB,垂足为E,BE=2,求弦CD的长.