题目内容
3.在平面直角坐标系中,横坐标与纵坐标都为整数的点叫整点,动点P从原点O出发,运动速度为每秒1个单位长度,规定P只能向上或向右运动,请回答下列问题:(1)填表
| 运动时间(秒) | 可得到的整点坐标 | 整点个数 |
| t=1 | (0,1)、(1,0) | 2 |
| t=2 | (0,2)、(2,0)、(1,1) | 3 |
| t=3 | (0,3)、(3,0)、(2,1)、(1,2) | 4 |
(3)当t=15时,可得到整点(8,7);
(4)当t=m+n时,可得到整点(m,n).
分析 (1)在坐标系中全部标出即可;
(2)由(1)可探索出规律,推出结果;
(3)可将图向右移8个单位,用8秒;再向上移动5个单位用5秒;
(4)可将图向右移m个单位,用8秒;再向上移动n个单位用5秒.
解答 解:(1)以1秒时达到的整数点为基准,向上或向右移动一格得到2秒时的可能的整数点;
再以2秒时得到的整数点为基准,向上或向右移动一格,得到3秒时可能得到的整数点,
故答案为:
| t=1 | (0,1)、(1,0) | 2 |
| t=2 | (0,2)、(2,0)、(1,1) | 3 |
| t=3 | (0,3)、(3,0)、(2,1)、(1,2) | 4 |
∴t=12秒时,应达到13个整数点,
故答案为13;
(3)横坐标为8,需要从原点开始沿x轴向右移动8秒,纵坐标为7,需再向上移动5秒,所以需要的时间为15秒,
故答案为15;
(4)横坐标为m,需要从原点开始沿x轴向右移动m秒,纵坐标为n,需再向上移动n秒,所以需要的时间为(m+n)秒.
故答案为:(m+n).
点评 此题主要考查了点的变化规律,解决本题的关键是掌握所给的方法,得到相应的可能的整数点的坐标.

练习册系列答案
相关题目
15.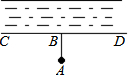 如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
 如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )| A. | 两点之间线段最短 | B. | 点到直线的距离 | ||
| C. | 两点确定一条直线 | D. | 垂线段最短 |
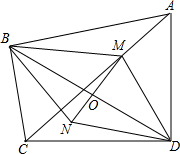 已知:如图所示,四边形ABCD中,∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO,并延长MO到N,使NO=MO,连接BN与ND.
已知:如图所示,四边形ABCD中,∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO,并延长MO到N,使NO=MO,连接BN与ND.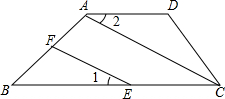 已知:如图,四边形ABCD中,AD∥BC,AC为对角线,点E在BC边上,点F在AB边上,且∠1=∠2.
已知:如图,四边形ABCD中,AD∥BC,AC为对角线,点E在BC边上,点F在AB边上,且∠1=∠2.