题目内容
11.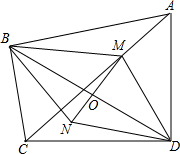 已知:如图所示,四边形ABCD中,∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO,并延长MO到N,使NO=MO,连接BN与ND.
已知:如图所示,四边形ABCD中,∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO,并延长MO到N,使NO=MO,连接BN与ND.(1)判断四边形BNDM的形状,并证明;
(2)若M是AC的中点,则四边形BNDM的形状又如何?说明理由.
分析 (1)由对角线互相平分的四边形是平行四边形即可得出结论;
(2)由直角三角形斜边上1的中线性质得出BM=$\frac{1}{2}$AC,DM=$\frac{1}{2}$AC,得出BM=DM,即可得出结论.
解答 (1)解:四边形BNDM是平行四边形,理由如下:
∵O是BD的中点,
∴OB=OD,
∵NO=MO,
∴四边形BNDM是平行四边形;
(2)解:四边形BNDM是菱形;理由如下:
∵∠ABC=∠ADC=90°,M是AC的中点,
∴BM=$\frac{1}{2}$AC,DM=$\frac{1}{2}$AC,
∴BM=DM,
∴四边形BNDM是菱形.
点评 本题考查了平行四边形的判定方法、直角三角形斜边上的中线性质、菱形的判定方法;熟练掌握平行四边形和菱形的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
1.三角形的三边a、b、c满足a(b-c)+2(b-c)=0,则这个三角形的形状是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
19.(-8)2014+(-8)2013能被下列数整除的是( )
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
3.在平面直角坐标系中,横坐标与纵坐标都为整数的点叫整点,动点P从原点O出发,运动速度为每秒1个单位长度,规定P只能向上或向右运动,请回答下列问题:
(1)填表
(2)当t=12时,整点有13个;
(3)当t=15时,可得到整点(8,7);
(4)当t=m+n时,可得到整点(m,n).
(1)填表
| 运动时间(秒) | 可得到的整点坐标 | 整点个数 |
| t=1 | (0,1)、(1,0) | 2 |
| t=2 | (0,2)、(2,0)、(1,1) | 3 |
| t=3 | (0,3)、(3,0)、(2,1)、(1,2) | 4 |
(3)当t=15时,可得到整点(8,7);
(4)当t=m+n时,可得到整点(m,n).
1.在发生“甲型H7N9禽流感”疫情期间,有专业机构认为在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
| A. | 甲地:总体平均数为3,中位数为4 | |
| B. | 乙地:中位数为2,众数为3 | |
| C. | 丙地:总体平均数为2,总体方差为3 | |
| D. | 丁地:总体平均数为1,总体方差大于0 |