题目内容
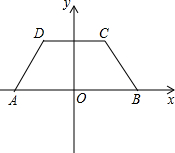 如图,在平面直角坐标系中,四边形ABCD是等腰梯形,底边AB在横轴上且原点O为AB中点,AB∥CD,∠DAB=60°,AB、BC(AB>BC)是方程x2-11x+28=0的两个根.
如图,在平面直角坐标系中,四边形ABCD是等腰梯形,底边AB在横轴上且原点O为AB中点,AB∥CD,∠DAB=60°,AB、BC(AB>BC)是方程x2-11x+28=0的两个根.(1)求点C的坐标;
(2)求线段AC的长;
(3)在x轴上是否存在一点P,在平面内有一点Q,使以点A、点C、点P、点Q为顶的四边形为菱形?若存在,请直接写出点Q的坐标?若不存在,请说明理由.
考点:四边形综合题
专题:
分析:(1)过C作CM⊥AB于M,求出方程的解,骑车AB、BC值,根据∠ABC=60°,求出CM、BM,即可求出答案;
(2)根据勾股定理求出AC即可;
(3)分为三种情况:①作AC得垂直平分线交直线CD于Q,此时Q符合,AQ=CQ,根据勾股定理求出CQ,即可得出答案;②以C为圆心,移AC为半径交直线CD于Q2、Q3,此时符合,求出CQ2=CQ3,得出即可;③作C关于直线AB的对称点Q4,此时Q4符合题意.
(2)根据勾股定理求出AC即可;
(3)分为三种情况:①作AC得垂直平分线交直线CD于Q,此时Q符合,AQ=CQ,根据勾股定理求出CQ,即可得出答案;②以C为圆心,移AC为半径交直线CD于Q2、Q3,此时符合,求出CQ2=CQ3,得出即可;③作C关于直线AB的对称点Q4,此时Q4符合题意.
解答:解:(1)
过C作CM⊥AB于M,
∵AB、BC(AB>BC)是方程x2-11x+28=0的两个根,
∴AB=7,BC=4,
∵四边形ABCD是等腰梯形,
∴∠DAB=∠B=60°,
∴BM=
BC=2,由勾股定理得:CM=2
,
∵O为AB中点,AB=7,
∴OA=OB=3.5,
∴OM=3.5-2=1.5,
即C的坐标是(1.5,2
);
(2)AM=OA+OM=3.5+1.5=5,CM=2
,
在Rt△AMC中,由勾股定理得:AC=
=
;
(3)在x轴上存在一点P,在平面内有一点Q,使以点A、点C、点P、点Q为顶的四边形为菱形,
理由是:①过A作AN⊥CD于N,作AC的垂直平分线交直线CD于Q,交AB于P,此时Q符合题意,

则设AQ=CQ=x,DN=BM=2,CD=7-2-2=3,
所以CR=DR=1.5
在Rt△ANQ中,AN=CM=2
,ND=3+2-x=5-x,AQ=x,由勾股定理得:(2
)2+(5-x)2=x2,
解得:x=2.7,
则QR=2.7-1.5=1.2,
即Q的坐标是(-1.2,2
);
②
以AC为边,如图2,Q2,Q3符合,过Q2作Q2W⊥AB于W,过Q3N⊥AB于N,
P2Q2=P3Q3=AC=
,Q2W=Q3N=2
,
由勾股定理得:P2W=P3N=
=5,
则OW=OA+AP2-P2W=3.5+
-5=
-1.5,ON=AP3+P3N-AO=
+5-3.5=
+1.5,
即Q2的 坐标是(1.5-
,2
),Q3的坐标是(
+1.5,2
);
③延长 CM到Q4,使CM=MQ4,此时Q4符合题意,如图3,

∵C(1.5,2
),
∴Q4的坐标是(1.5,-2
).

过C作CM⊥AB于M,
∵AB、BC(AB>BC)是方程x2-11x+28=0的两个根,
∴AB=7,BC=4,
∵四边形ABCD是等腰梯形,
∴∠DAB=∠B=60°,
∴BM=
| 1 |
| 2 |
| 3 |
∵O为AB中点,AB=7,
∴OA=OB=3.5,
∴OM=3.5-2=1.5,
即C的坐标是(1.5,2
| 3 |
(2)AM=OA+OM=3.5+1.5=5,CM=2
| 3 |
在Rt△AMC中,由勾股定理得:AC=
52+(2
|
| 37 |
(3)在x轴上存在一点P,在平面内有一点Q,使以点A、点C、点P、点Q为顶的四边形为菱形,
理由是:①过A作AN⊥CD于N,作AC的垂直平分线交直线CD于Q,交AB于P,此时Q符合题意,

则设AQ=CQ=x,DN=BM=2,CD=7-2-2=3,
所以CR=DR=1.5
在Rt△ANQ中,AN=CM=2
| 3 |
| 3 |
解得:x=2.7,
则QR=2.7-1.5=1.2,
即Q的坐标是(-1.2,2
| 3 |
②

以AC为边,如图2,Q2,Q3符合,过Q2作Q2W⊥AB于W,过Q3N⊥AB于N,
P2Q2=P3Q3=AC=
| 37 |
| 3 |
由勾股定理得:P2W=P3N=
(
|
则OW=OA+AP2-P2W=3.5+
| 37 |
| 37 |
| 37 |
| 37 |
即Q2的 坐标是(1.5-
| 37 |
| 3 |
| 37 |
| 3 |
③延长 CM到Q4,使CM=MQ4,此时Q4符合题意,如图3,

∵C(1.5,2
| 3 |
∴Q4的坐标是(1.5,-2
| 3 |
点评:本题考查了勾股定理,菱形的性质,轴对称的性质,等腰梯形的性质的应用,综合性比较强,用了分类讨论思想,难度偏大.

练习册系列答案
相关题目
据统计,截止10月8日北京颐和园的入园人数为805万,这个数字用科学记数法表示为( )
| A、8×106 |
| B、8.05×106 |
| C、805×104 |
| D、8.05×107 |
 休博园内有两展览馆中国国家馆A和外国国家馆B,展馆外围有两条小道L1和L2(如图所示),现由于展馆人多天气炎热,故决定再建一个休息区C,要求休息区到两个展馆A和B的距离相等且到两条小路的距离也相等,请用直尺和圆规作图找出休息区C的位置.
休博园内有两展览馆中国国家馆A和外国国家馆B,展馆外围有两条小道L1和L2(如图所示),现由于展馆人多天气炎热,故决定再建一个休息区C,要求休息区到两个展馆A和B的距离相等且到两条小路的距离也相等,请用直尺和圆规作图找出休息区C的位置.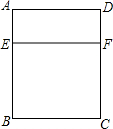 用7m长的铝合金做成透光面积(矩形ABCD的面积)为2m2的“日”型窗框(BC不超过1.3m),求窗框的宽度?(铝合金的宽度忽略不计)
用7m长的铝合金做成透光面积(矩形ABCD的面积)为2m2的“日”型窗框(BC不超过1.3m),求窗框的宽度?(铝合金的宽度忽略不计) 如图,在矩形ABCD中,CE⊥BD于E,∠DCE:∠BCE=3:1,且M为OC的中点,试说明:ME⊥AC.
如图,在矩形ABCD中,CE⊥BD于E,∠DCE:∠BCE=3:1,且M为OC的中点,试说明:ME⊥AC.