题目内容
 如图,在矩形ABCD中,CE⊥BD于E,∠DCE:∠BCE=3:1,且M为OC的中点,试说明:ME⊥AC.
如图,在矩形ABCD中,CE⊥BD于E,∠DCE:∠BCE=3:1,且M为OC的中点,试说明:ME⊥AC.考点:矩形的性质,等腰直角三角形
专题:证明题
分析:设∠BCE=x°,由条件得:x=
°.而∠BCE=∠BDC=x,所以∠BOC=2x=
°,而∠ECO=90-(∠DCO+∠BCE)=90°-2x=
°,所以∠BOC=∠ECO即△OCE为等腰三角形,M为OC中点,所以EM⊥AC.
| 90 |
| 4 |
| 90 |
| 2 |
| 90 |
| 2 |
解答:证明:设∠BCE=x°,
∵四边形ABCD是矩形,
∴∠DCB=90°,
∴∠DCE+∠BCE=90°,
又∵∠DCE:∠BCE=1:3,
∴∠OCE=45°,
∵CE⊥BD,
∴△OEC为等腰直角三角形,
∵M为OC中点,
∴ME⊥AC,
∵四边形ABCD是矩形,
∴∠DCB=90°,
∴∠DCE+∠BCE=90°,
又∵∠DCE:∠BCE=1:3,
∴∠OCE=45°,
∵CE⊥BD,
∴△OEC为等腰直角三角形,
∵M为OC中点,
∴ME⊥AC,
点评:本题考查了矩形的性质、等腰直角三角形的判定和性质,题目的综合性较强,难度一般,是常见的中考题型.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 如图,△ABC和△DEF的顶点都在方格的顶点上,请按下列要求画图.
如图,△ABC和△DEF的顶点都在方格的顶点上,请按下列要求画图. 如图,若一次函数y=kx+b与反比例函数
如图,若一次函数y=kx+b与反比例函数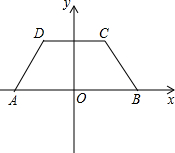 如图,在平面直角坐标系中,四边形ABCD是等腰梯形,底边AB在横轴上且原点O为AB中点,AB∥CD,∠DAB=60°,AB、BC(AB>BC)是方程x2-11x+28=0的两个根.
如图,在平面直角坐标系中,四边形ABCD是等腰梯形,底边AB在横轴上且原点O为AB中点,AB∥CD,∠DAB=60°,AB、BC(AB>BC)是方程x2-11x+28=0的两个根. 如图,矩形ABCD中,AB=6,BC=8,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F,PE+PF的值是多少?
如图,矩形ABCD中,AB=6,BC=8,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F,PE+PF的值是多少?