题目内容
定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“凤凰”方程.已知ax2+bx+c=0(a≠0)是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是( )
A. a=c B. a=b C. b=c D. a=b=c
A 解:∵一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根,
∴△=b2﹣4ac=0,
又a+b+c=0,即b=﹣a﹣c,
代入b2﹣4ac=0得(﹣a﹣c)2﹣4ac=0,
即(a+c)2﹣4ac=a2+2ac+c2﹣4ac=a2﹣2ac+c2=(a﹣c)2=0,
∴a=c.
故选A

练习册系列答案
相关题目
 图象上的概率.
图象上的概率.
 B. 2 C. 4
B. 2 C. 4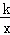 (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).
(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).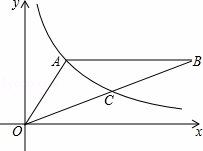

 B.
B.  C.
C.  D.
D. 


 ﹣
﹣ ,其中a=1.
,其中a=1. ,则AB的长为( )
,则AB的长为( )