Question

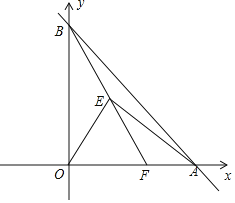
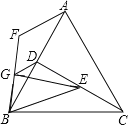
【题目】如图，已知等边△ABC，CD⊥AB于D，AF⊥AC，E为线段CD上一点，且CE＝AF，连接BE，BF，EG⊥BF于G，连接DG．

（1）求证：BE＝BF；

（2）试说明DG与AF的位置关系和数量关系．

Answer 1

【答案】（1）见解析；（2）AF＝2GD，AF∥DG.

【解析】

（1）由等边三角形的性质可得AB=AC=BC，∠BAC=∠ACB=∠ABC=60°，BD=AD，∠BCD=30°，由“SAS”可证△ABF≌△CBE，可得BF=BE；
（2）通过证明△BEF是等边三角形，可得BG=GF，由三角形中位线定理可得AF=2GD，AF∥DG．

证明：（1）∵△ABC是等边三角形

∴AB＝AC＝BC，∠BAC＝∠ACB＝∠ABC＝60°

∵CD⊥AB，AC＝BC

∴BD＝AD，∠BCD＝30°，

∵AF⊥AC

∴∠FAC＝90°

∴∠FAB＝∠FAC﹣∠BAC＝30°

∴∠FAB＝∠ECB，且AB＝BC，AF＝CE

∴△ABF≌△CBE（SAS）

∴BF＝BE

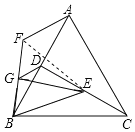
（2）AF＝2GD，AF∥DG

理由如下：连接EF，

∵△ABF≌△CBE

∴∠ABF＝∠CBE，

∵∠ABE+∠EBC＝60°

∴∠ABE+∠ABF＝60°，且BE＝BF

∴△BEF是等边三角形，且GE⊥BF

∴BG＝FG，且BD＝AD

∴AF＝2GD，AF∥DG