题目内容
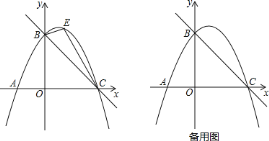
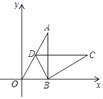
【题目】如图，直线
经过点A，作AB⊥x轴于点B，将△ABO绕点B顺时针旋转60°得到△CBD，若点B的坐标为（1，0），则点C的坐标为（ ）
A.（3，
）B.（
，）C.（3，
）D.（，）
【答案】D
【解析】
过C作CE⊥x轴于E，得出∠ABO＝90°，再利用旋转的性质得出△BDO是等边三角形，然后利用等边三角形的性质，即可解答．
解：如图，过C作CE⊥x轴于E，则∠BEC＝90°，
∵点B的坐标为（1，0），直线
经过点A，AB⊥x轴，
∴OB＝1，AB＝
，∠ABO＝90°，
由旋转可得，BC＝AB＝，OB＝DB，∠DBO＝60°，∠DBC＝90°，
∴△BDO是等边三角形，
∴∠CBE＝90°﹣60°＝30°，
∴CE＝
BC＝，BE＝CE＝
，
∴OE＝1+＝
，
∴点C的坐标为（，
），
故选：D．
练习册系列答案
相关题目
