题目内容
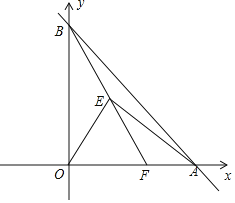
【题目】如图,在直角坐标系中,直线![]() 与x轴正半轴,y轴正半轴分别交于点A,B,点
与x轴正半轴,y轴正半轴分别交于点A,B,点![]() ,点E在第一象限,
,点E在第一象限,![]() 为等边三角形,连接AE,BE
为等边三角形,连接AE,BE
![]() 求点E的坐标;
求点E的坐标;
![]() 当BE所在的直线将
当BE所在的直线将![]() 的面积分为3:1时,求
的面积分为3:1时,求![]() 的面积;
的面积;
![]() 取线段AB的中点P,连接PE,OP,当
取线段AB的中点P,连接PE,OP,当![]() 是以OE为腰的等腰三角形时,则
是以OE为腰的等腰三角形时,则![]() ______
______![]() 直接写出b的值
直接写出b的值![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
![]() 根据等边三角形的性质可得高线EC的长,可得E的坐标;
根据等边三角形的性质可得高线EC的长,可得E的坐标;
![]() 如图2,当BE所在的直线将
如图2,当BE所在的直线将![]() 的面积分为3:1时,存在两种情况:
的面积分为3:1时,存在两种情况:![]() 如图2,
如图2,![]() :
:![]() :1,即OD:
:1,即OD:![]() :1,
:1,![]() :
:![]() :3,即OD:
:3,即OD:![]() :3,先确认DE的解析式,可得OA和OB的长,根据面积差可得结论;
:3,先确认DE的解析式,可得OA和OB的长,根据面积差可得结论;
![]() 存在两种情况:
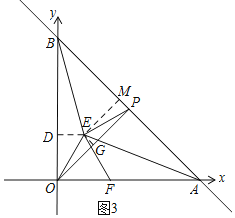
存在两种情况:![]() 如图3,
如图3,![]() ,作辅助线,构建矩形和高线ED和EM,根据三角形AOB面积的两种求法列等式可得b的值,
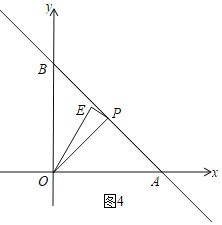
,作辅助线,构建矩形和高线ED和EM,根据三角形AOB面积的两种求法列等式可得b的值,![]() 如图4,
如图4,![]() ,根据等腰三角形和等边三角形的性质可得b的值.
,根据等腰三角形和等边三角形的性质可得b的值.
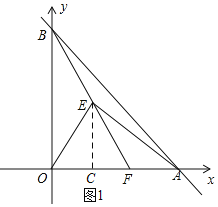
解:![]() 如图1,过E作
如图1,过E作![]() 轴于C,
轴于C,
![]() 点
点![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 当BE所在的直线将
当BE所在的直线将![]() 的面积分为3:1时,存在两种情况:
的面积分为3:1时,存在两种情况:
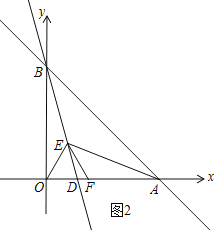
![]() 如图2,
如图2,![]() :
:![]() :1,即OD:
:1,即OD:![]() :1,
:1,
![]() ,
,
![]() ,
,
![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
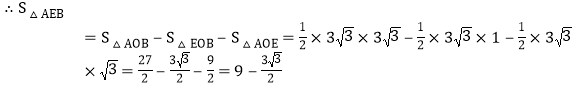 ;
;
![]() :
:![]() :3,即OD:
:3,即OD:![]() :3,
:3,
![]() ,
,
![]() ,
,
![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,
![]() 点B在y轴正半轴上,
点B在y轴正半轴上,
![]() 此种情况不符合题意;
此种情况不符合题意;
综上,![]() 的面积是
的面积是![]() ;
;
![]() 存在两种情况:
存在两种情况:
![]() 如图3,
如图3,![]() ,过E作
,过E作![]() 轴于D,作
轴于D,作![]() 于M,作
于M,作![]() 于G,
于G,
![]() 是等腰直角三角形,P是AB的中点,
是等腰直角三角形,P是AB的中点,
![]() ,
,
![]() ,
,
![]() 四边形EGPM是矩形,
四边形EGPM是矩形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 如图4,当
如图4,当![]() 时,则
时,则![]() ,
,
![]() 是等腰直角三角形,P是AB的中点,
是等腰直角三角形,P是AB的中点,
![]() ,
,
![]() ,即
,即![]() ,
,
故答案为:![]() 或
或![]() .
.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目








