Question

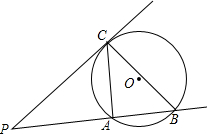如图 P是⊙O外一点，过点P作直线PA与⊙O相交，交点为A、B，作直线PC与⊙O相切，切点为C，连接AC、AD．
（1）求证：∠PCA=∠PBC；
（2）如果PA=3，PB=5，求PC的长．

Answer 1

考点：切线的性质

专题：

分析：（1）如图，作辅助线，运用切线的性质定理及圆周角定理问题即可解决；
（2）直接运用切割线定理问题即可解决．

解答：解：（1）如图，连接OA、OC；
∵PC与⊙O相切，
∴OC⊥PC，
∴∠PCA=90°-∠OCA；
∵OA=OC，
∴∠OCA=∠OAC；
∴∠AOC=180°-2∠OCA；
∵∠PBC=

1

2

∠AOC，
∴∠PBC=90°-∠OC，
∴∠PCA=∠PBC．
（2）由切割线定理得：
PC²=PA•PB，
∵PA=3，PB=5，
∴PC=

15

．

点评：该命题主要考查了切线的性质及其应用问题；解题的关键是作辅助线，灵活运用有关定理来分析、判断、推理或解答．