题目内容
已知实数x,y满足:①y-2x=5;②(2x+3)(y+1)<2xy+10.若k为正整数,y为整数,试比较代数式k2y+9y与代数式3k2+3y2值的大小.
考点:解一元一次不等式,代数式求值
专题:计算题
分析:由y-2x=5得y=2x+5,则(2x+3)(2x+5+1)<2x(2x+5)+10,解此一元一次不等式得x<-1,所以
<-1,解得y<3,由于k2y+9y-(3k2+3y2)=k2y+9y-3k2-3y2=(y-3)(k2-3y),然后讨论:由于k为正整数,y为小于3的整数,当y为非正整数时或当y=1,k=1或当y=1,k=2或当y=2,k=1、2或当k>2的整数时,分别比较它们的大小.
| y-5 |
| 2 |
解答:解:∵y-2x=5,
∴y=2x+5,
∴(2x+3)(2x+5+1)<2x(2x+5)+10,即得x<-1,
而x=
,
∴
<-1,
∴y<3,
k2y+9y-(3k2+3y2)=k2y+9y-3k2-3y2
=k2(y-3)-3y(y-3)
=(y-3)(k2-3y),
∵k为正整数,y为小于3的整数,
∴当y为非正整数时,k2y+9y-(3k2+3y2)<0,即k2y+9y<3k2+3y2,
当y=1,k=1,k2y+9y>3k2+3y2,
当y=1,k=2,k2y+9y<3k2+3y2,
当y=2,k=1或2,k2y+9y>3k2+3y2,
当k>2的整数时,k2y+9y<3k2+3y2.
∴y=2x+5,
∴(2x+3)(2x+5+1)<2x(2x+5)+10,即得x<-1,
而x=
| y-5 |
| 2 |
∴
| y-5 |
| 2 |
∴y<3,
k2y+9y-(3k2+3y2)=k2y+9y-3k2-3y2
=k2(y-3)-3y(y-3)
=(y-3)(k2-3y),
∵k为正整数,y为小于3的整数,
∴当y为非正整数时,k2y+9y-(3k2+3y2)<0,即k2y+9y<3k2+3y2,
当y=1,k=1,k2y+9y>3k2+3y2,
当y=1,k=2,k2y+9y<3k2+3y2,
当y=2,k=1或2,k2y+9y>3k2+3y2,
当k>2的整数时,k2y+9y<3k2+3y2.
点评:本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式.

练习册系列答案
相关题目
 如图,A、P、B、C是同圆上的四个点,∠APB=120°,PC平分∠APB.求证:△ABC是等边三角形.
如图,A、P、B、C是同圆上的四个点,∠APB=120°,PC平分∠APB.求证:△ABC是等边三角形.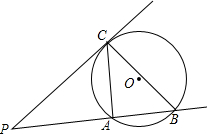 如图 P是⊙O外一点,过点P作直线PA与⊙O相交,交点为A、B,作直线PC与⊙O相切,切点为C,连接AC、AD.
如图 P是⊙O外一点,过点P作直线PA与⊙O相交,交点为A、B,作直线PC与⊙O相切,切点为C,连接AC、AD.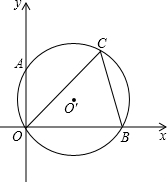 如图所示,已知CO、CB是⊙O′的弦,⊙O′与平面直角坐标系的x轴、y轴分别相交于点B、A,若∠COB=45°,∠OBC=75°,点A的坐标为(0,2),求⊙O′的直径.
如图所示,已知CO、CB是⊙O′的弦,⊙O′与平面直角坐标系的x轴、y轴分别相交于点B、A,若∠COB=45°,∠OBC=75°,点A的坐标为(0,2),求⊙O′的直径.