题目内容
19．（1）计算：-$\sqrt{2}$+$\sqrt{24}$×$\sqrt{\frac{1}{3}}$（2）解方程：3x（x+4）=2（x+4）
分析 （1）先化简二次根式、二次根式的乘法运算，然后计算加减法；
（2）先移项，再提取公因式即可得出x的值．
解答 解：（1）原式=-$\sqrt{2}$+2$\sqrt{2}$=$\sqrt{2}$；
（2）由原方程，得
（3x-2）（x+4）=0，
所以3x-2=0或x+4=0，
解得x1=$\frac{2}{3}$，x2=-4．
点评 本题考查了解一元二次方程-因式分解法，二次根式的混合运算．因式分解法就是先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．
练习册系列答案
全能测控期末小状元系列答案
相关题目
如图，在△ABC中，∠A=50°，点O是△ABC三边垂直平分线的交点，则∠BOC=100°．
一个小立方体的六面分别标有字母A，B，C，D，E，F，如图是从三个不同方向看到的情形，则字母A对面的字母是C，字母D对面的字母是B．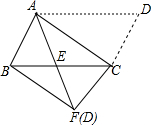
如图，将?ABCD沿对角线AC进行折叠，折叠后点D落在点F处，AF交BC于点E，有下列结论：①△ABF≌△CFB；②AE=CE；③BF∥AC；④BE=CE，其中正确结论的个数是（ ）
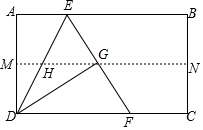如图，四边形ABCD是矩形纸片，AB=2，对折矩形纸片ABCD，使AD与BC重合，折痕为MN，展平后再过点B折叠矩形纸片，使点A落在MN上的点G处，折痕BE与MN相交于点H；再次展平，连接BG，EG，延长EG交BC于点F．有如下结论：
如图所示，已知一次函数y=2x+b的图象与x轴的交点坐标为（-2，0），则不等式2x+b＞0的解集为x＞-2．