题目内容
4．三角形的三边长a，b，c满足关系式（a+2b-60）2+|b-18|+$\sqrt{c-30}$=0，则这个三角形是（ ）| A． | 锐角三角形 | B． | 钝角三角形 | C． | 等腰三角形 | D． | 直角三角形 |
分析 先求出a、b、c的值，再根据勾股定理的逆定理求出三角形是直角三角形，即可得出选项．
解答 解：∵（a+2b-60）2+|b-18|+$\sqrt{c-30}$=0，
∴a+2b-60=0，b-18=0，c-30=0，
∴a=24，b=18，c=30，
∴a2+b2=c2，
∴这个三角形是直角三角形，
故选D．
点评 本题考查了勾股定理的逆定理，绝对值、偶次方、算术平方根的非负性等知识点，能熟记勾股定理的逆定理的内容是解此题的关键，如果一个三角形的两边a、b的平方和等于第三边c的平方，那么这个三角形是直角三角形．
练习册系列答案
相关题目
14．刘亮的妈妈每天早上要送新鲜蔬菜到市场去卖，下面是她一周送出的20筐菜的重量记录表，每筐以25kg为标准重量．
求她一周送出20筐新鲜蔬菜的总质量．
| 筐数 | 2 | 5 | 3 | 4 | 2 | 4 |
| 与标准质量相比（kg） | -0.8 | +0.6 | -0.5 | +0.4 | +0.5 | -0.3 |
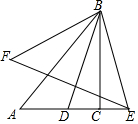如图，在Rt△BAC中，∠ACB=Rt∠，AC=6，BC=8，D是AC边上的一点，点D关于BC的对称点为E，关于AB的对称点为F，连接BD，BE，BF，EF，若BD平分∠ABC，则EF的长为$\frac{16}{5}\sqrt{10}$．
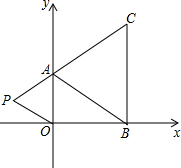在如图直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a，b，c满足关系$\sqrt{a-2}+（b-3）^{2}$=0，（c-4）2≤0，点P、点A、点C在同一条直线上．
9．已知方程|x-a|+|x+a|=a有解，那么有理数a的值是（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | 不能确定 |
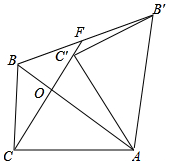如图，在Rt△ABC中，∠ACB=90°，tan∠CBA=$\frac{4}{3}$，AB=5．将△ABC绕点A顺时针旋转得到△AB′C′，连接CC′并延长，交AB于点O，交BB′于点F．若CC′=CA，则BF=$\frac{5}{2}$．
13．下列说法不正确的是（ ）
| A． | 1的算术平方根是1 | B． | 4的平方根是±2 | ||
| C． | -9的立方根是-3 | D． | -5的平方是25 |
14．根据调查，某地区一周空气质量报告中每天空气污染指数如下表所示，这组数据的众数是（ ）
| 检测时间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 空气污染指数 | 21 | 22 | 21 | 24 | 20 | 22 | 21 |
| A． | 20 | B． | 21 | C． | 22 | D． | 24 |