题目内容
20．
解不等式组$\left\{\begin{array}{l}{-2x＜6①}\\{3（x+1）≤2x+5②}\end{array}\right.$，并将解集在数轴上表示出来．
分析 分别求出各不等式的解集，再求出其公共解集并在数轴上表示出来即可．
解答 解：$\left\{\begin{array}{l}{-2x＜6①}\\{3（x+1）≤2x+5②}\end{array}\right.$，
由①得，x＞-3，
由②得，x≤2，
故此不等式组的解集为：-3＜x≤2．
在数轴上表示为：
点评 本题考查的是解一元一次不等式组，熟知“同大取较大，同小取较小，小大大小中间找，大大小小解不了”的原则是解答此题的关键．
练习册系列答案
相关题目
10．
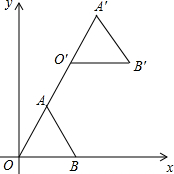如图，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（2，0），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为（ ）
如图，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（2，0），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为（ ）| A． | （4，2$\sqrt{3}$） | B． | （3，3$\sqrt{3}$） | C． | （4，3$\sqrt{3}$） | D． | （3，2$\sqrt{3}$） |
11．
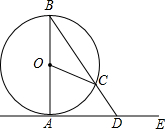如图，AB是⊙O直径，点C在⊙O上，AE是⊙O的切线，A为切点，连接BC并延长交AE于点D．若∠AOC=80°，则∠ADB的度数为（ ）
如图，AB是⊙O直径，点C在⊙O上，AE是⊙O的切线，A为切点，连接BC并延长交AE于点D．若∠AOC=80°，则∠ADB的度数为（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 20° |
8．一个不透明的布袋中，放有3个白球，5个红球，它们除颜色外完全相同，从中随机摸取1个，摸到红球的概率是（ ）
| A． | $\frac{5}{8}$ | B． | $\frac{1}{5}$ | C． | $\frac{3}{8}$ | D． | $\frac{1}{3}$ |
5．
如图是一个可以自由转动的正六边形转盘，其中三个正三角形涂有阴影，转动指针，指针落在有阴影的区域内的概率为a，如果投掷一枚硬币，正面向上的概率为b，关于a、b大小的正确判断是（ ）
如图是一个可以自由转动的正六边形转盘，其中三个正三角形涂有阴影，转动指针，指针落在有阴影的区域内的概率为a，如果投掷一枚硬币，正面向上的概率为b，关于a、b大小的正确判断是（ ）| A． | a＞b | B． | a=b | C． | a＜b | D． | 不能判断 |
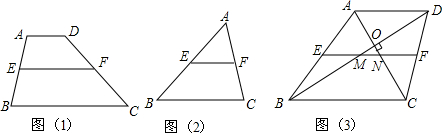
12．下列四个图形中，线段BE是△ABC的高的是（ ）
| A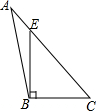． |  | B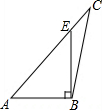． |  | C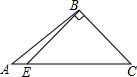． |  | D． |  |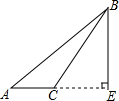
