题目内容
2．已知一个多边形的每一个外角都相等，一个内角与一个外角的度数之比为7：2，则这个多边形的边数为9．分析 这个多边形的一个内角与一个外角的和是180°，然后求得这个多边形的一个外角的度数为40°，然后由360°÷40°=9可求得答案．
解答 解：∵多边形的每一个外角都相等，
∴它的每个内角都相等．
设它的一个内角为7x，一个外角和为2x．
根据题意得：7x+2x=180°．
解得：x=20°．
∴2x=2×20°=40°．
360°÷40°=9．
故答案为：9．
点评 本题主要考查的是多边形的内角与外角，掌握正多边形的一个内角与一个外角的和是180°是解题的关键．
练习册系列答案
相关题目
17．将2x2-x-2分解因式为（ ）
| A． | $（{x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}}）（{x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}}）$ | B． | $2（{x+\frac{1}{4}-\frac{{\sqrt{17}}}{4}}）（{x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}}）$ | ||
| C． | $2（{x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}}）（{x+\frac{1}{4}-\frac{{\sqrt{17}}}{4}}）$ | D． | $2（{x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}}）（{x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}}）$ |
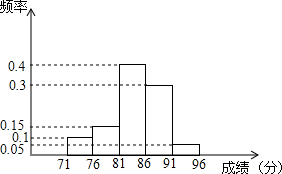为了了解某校初三年级200名学生的数学毕业考试成绩，从中抽取了20名学生的数学成绩进行分析，下面是根据这20名学生的数学成绩画出的频数分布直方图，如图根据题中给出的条件回答下列问题：
如图所示，?ABCD中，∠ADC和∠BCD的平分线交于点M，且分别交AB于E、F．
已知在纸面上有一数轴（如图），折叠纸面．