题目内容
13.在△ABC中,CD⊥AB,垂足为D,CA=4,CB=9,CD=3,则△ABC的外接圆面积等于36π.分析 由三角函数求出sinB=$\frac{CD}{BC}$=$\frac{1}{3}$,由正弦定理得出$\frac{AC}{sinB}$=2R(R为△ABC的外接圆半径),求出半径R,即可得出结果.
解答 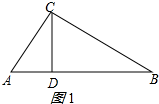 解:如图1.2所示:
解:如图1.2所示:
∵CD⊥AB,
∴∠CDB=90°,
∴sinB=$\frac{CD}{BC}$=$\frac{3}{9}$=$\frac{1}{3}$,
由正弦定理得:$\frac{AC}{sinB}$=2R(R为△ABC的外接圆半径), ∴2R=$\frac{AC}{sinB}$=$\frac{4}{\frac{1}{3}}$=12
∴2R=$\frac{AC}{sinB}$=$\frac{4}{\frac{1}{3}}$=12
∴R=6,
∴△ABC的外接圆面积=π•R2=π×62=36π,
故答案为:36π.
点评 本题考查了三角形的外接圆、三角函数、正弦定理;由三角函数和正弦定理求出三角形的外接圆半径是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.若方程x-(2a+1)=3x+(3a+2)的解是x=0,则a等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{3}{5}$ |
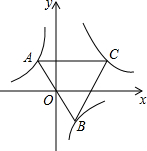 如图,已知点A是双曲线y=-$\frac{2}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是6.
如图,已知点A是双曲线y=-$\frac{2}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是6.
 如图,甲楼每层高都是3.1米,乙楼高40米,从甲楼的第6层往外看乙楼楼顶,仰角为30°,两楼相距AB有多少米?(结果精确到0.1米)
如图,甲楼每层高都是3.1米,乙楼高40米,从甲楼的第6层往外看乙楼楼顶,仰角为30°,两楼相距AB有多少米?(结果精确到0.1米) 已知一次函数y=kx+b的图象如图,当x<0时,y的取值范围是y>2.
已知一次函数y=kx+b的图象如图,当x<0时,y的取值范围是y>2.