题目内容
20.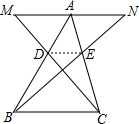 如图,MN经过△ABC的顶点A,MN∥BC,AM=AN,MC交AB于D,NB交AC于E.
如图,MN经过△ABC的顶点A,MN∥BC,AM=AN,MC交AB于D,NB交AC于E.(1)求证:DE∥BC.
(2)连结DE,如果DE=1,BC=3,求AN的长.
分析 (1)由平行线分线段成比例结合条件可证得$\frac{AD}{BD}=\frac{AE}{CE}$,即可得出结论;
(2)由(1)的结论,结合平行线分线段成比例可得到$\frac{AD}{AB}=\frac{DE}{BC}$=$\frac{1}{3}$,得出$\frac{AD}{BD}$=$\frac{1}{2}$,即$\frac{AN}{BC}=\frac{AE}{CE}$=$\frac{1}{2}$,得出AN=$\frac{1}{2}$BC=$\frac{3}{2}$即可.
解答 (1)证明:∵MN∥BC,
∴$\frac{AM}{BC}=\frac{AD}{BD}$,$\frac{AN}{BC}=\frac{AE}{CE}$,
∵AM=AN,
∴$\frac{AD}{BD}=\frac{AE}{CE}$,
∴DE∥BC;
(2)解:∵DE∥BC,
∴$\frac{AD}{AB}=\frac{DE}{BC}$=$\frac{1}{3}$,
∴$\frac{AD}{BD}$=$\frac{1}{2}$,
即$\frac{AN}{BC}=\frac{AE}{CE}$=$\frac{1}{2}$,
∴AN=$\frac{1}{2}$BC=$\frac{3}{2}$.
点评 本题主要考查平行线分线段成比例的性质和判定;掌握线段对应成比例?两直线平行是解题的关键.

练习册系列答案
相关题目
8.若方程x-(2a+1)=3x+(3a+2)的解是x=0,则a等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{3}{5}$ |
 如图,已知A,B,C,D四点共圆,且AC=BC.求证:DC平分∠BDE.
如图,已知A,B,C,D四点共圆,且AC=BC.求证:DC平分∠BDE.