题目内容
17.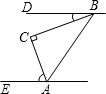 如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=22°,则∠CAE的度数是68°.
如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=22°,则∠CAE的度数是68°.
分析 过点C作CF∥AE,根据平行公理可得CF∥BD,然后根据两直线平行内错角相等可得∠BCF=∠DBC,然后求出∠ACF,再根据两直线平行,内错角相等可得∠CAE=∠ACF.
解答  解:如图,过点C作CF∥AE,
解:如图,过点C作CF∥AE,
∵BD∥AE,
∴CF∥BD,
∴∠BCF=∠DBC=22°,
∵∠C=90°,
∴∠ACF=90°-∠BCF=90°-22°=68°,
∵CF∥AE,
∴∠CAE=∠ACF=68°.
故答案为:68°.
点评 本题考查了平行线的性质,此类题目,难点在于过拐点作平行线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.一次函数y=(3m-2)x+2m-1的图象交于y轴的正半轴,则m的取值范围是( )
| A. | m>$\frac{2}{3}$ | B. | m>$\frac{1}{2}$ | C. | m<$\frac{1}{2}$ | D. | m<$\frac{2}{3}$ |
12.下列运算正确的是( )
| A. | $\sqrt{2016}$+$\sqrt{2016}$=$\sqrt{4032}$ | B. | $\sqrt{201{6}^{2}-(\frac{1}{2016})^{2}}=2016-\frac{1}{2016}$ | ||
| C. | $\sqrt{2016}×\sqrt{4032}$=2016$\sqrt{2}$ | D. | $\sqrt{2016}÷\sqrt{2}=1008$ |
2.下列运算中,结果等于a5的是( )
| A. | a2+a3 | B. | a10÷a2 | C. | a3•a2 | D. | (a2)3 |
9.在Rt△ABC中,∠C=90°,若AB=6,BC=2,则cosB=( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{3\sqrt{2}}{4}$ |
6.若x=3是关于x的方程x2-bx-3a=0的一个根,则a+b的值为( )
| A. | 3 | B. | -3 | C. | 9 | D. | -9 |
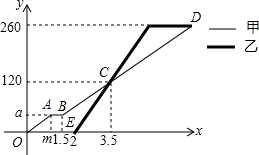 甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,甲机器先开始工作,中途停机检修了0.5小时.如图是甲、乙两台机器在整个工作过程中各自加工的零件个数y(个)与甲机器工作时间x(时)之间的函数图象.
甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,甲机器先开始工作,中途停机检修了0.5小时.如图是甲、乙两台机器在整个工作过程中各自加工的零件个数y(个)与甲机器工作时间x(时)之间的函数图象.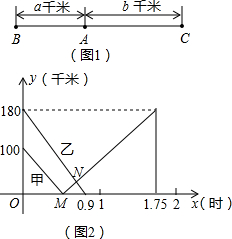 金温高铁于2015年12月26日正式开通,且被誉为“浙江最美高铁”的线路.如图1所示,已知金温高铁上有A,B,C三站,B,C两站相距280千米,甲、乙两列动车分别从B,C两站同时沿铁路匀速相向出发向终点站C,B而行,甲、乙两动车离A站的距离y(千米)与行驶时间x(时)的关系如图2所示,很据图象,解答以下问题:
金温高铁于2015年12月26日正式开通,且被誉为“浙江最美高铁”的线路.如图1所示,已知金温高铁上有A,B,C三站,B,C两站相距280千米,甲、乙两列动车分别从B,C两站同时沿铁路匀速相向出发向终点站C,B而行,甲、乙两动车离A站的距离y(千米)与行驶时间x(时)的关系如图2所示,很据图象,解答以下问题: