题目内容
3.在?ABCD中,对角线AC与BD交于点O,若?ABCD的面积是16m2,则△AOB的面积是4m2.分析 因为平行四边形的对角线互相平分,所以平行四边形被对角线分成的四部分的面积相等,即?ABCD的面积=△AOB的面积×4,即可得出结果.
解答 解: ∵点O是平行四边形ABCD的对角线AC和BD的交点,
∵点O是平行四边形ABCD的对角线AC和BD的交点,
∴OA=OC,OB=OD,
在△AOB与△COD中,$\left\{\begin{array}{l}{OA=OC}&{\;}\\{∠AOB=∠COD}&{\;}\\{OB=OD}&{\;}\end{array}\right.$,
∴△AOB≌△COD(SAS).
同理,△BOC≌△DOA.
又∵AO是△ABD的中线,
∴△AOB与△AOD的面积相等,
故?ABCD的面积=△AOB的面积×4,
∴△AOB的面积=16÷4=4(m2).
故答案是:4m2.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质.解题时,充分利用了平行四边形的对角线互相平分的性质.

练习册系列答案
相关题目
13. 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
14.下列实数中,介于5和6之间的是( )
| A. | $\sqrt{21}$ | B. | $\sqrt{30}$ | C. | $\sqrt{47}$ | D. | $\root{3}{39}$ |
18.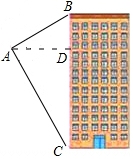 如图,热气球从空中的A处看一栋楼的顶部仰角为30°,看这栋楼的俯角为60°.热气球与楼的水平距离为120m.这栋楼的高度为( )
如图,热气球从空中的A处看一栋楼的顶部仰角为30°,看这栋楼的俯角为60°.热气球与楼的水平距离为120m.这栋楼的高度为( )
 如图,热气球从空中的A处看一栋楼的顶部仰角为30°,看这栋楼的俯角为60°.热气球与楼的水平距离为120m.这栋楼的高度为( )
如图,热气球从空中的A处看一栋楼的顶部仰角为30°,看这栋楼的俯角为60°.热气球与楼的水平距离为120m.这栋楼的高度为( )| A. | 160m | B. | 160$\sqrt{3}$m | C. | (160-160$\sqrt{3}$)m | D. | 360m |
15.不等式$\frac{x}{2}$$-\frac{x-1}{3}$≤1的解集是( )
| A. | x≥-1 | B. | x≤-1 | C. | x≥4 | D. | x≤4 |
12.下列事件:①在体育中考中,小明考了满分;②经过有交通信号灯的路口,遇到红灯;③抛掷两枚正方体骰子,点数和大于1;④度量任一三角形,其外角和都是180°,其中必然事件是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
13.下列调查适合普查的是( )
| A. | 调查2017年2月份利辛市场上某品牌饮料的质量 | |
| B. | 调查某月份长江安徽段水域的水质量情况 | |
| C. | 光明节能厂检测一批新型节能灯的使用寿命 | |
| D. | 了解某班50名学生的年龄情况 |
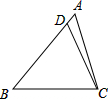 在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2$\sqrt{2}$,AB=3,则AD=$\frac{1}{3}$.
在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2$\sqrt{2}$,AB=3,则AD=$\frac{1}{3}$.