题目内容
12.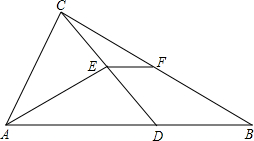 如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD于点E,F是BC的中点,求证:EF=$\frac{1}{2}$(AB-AC).
如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD于点E,F是BC的中点,求证:EF=$\frac{1}{2}$(AB-AC).
分析 由等腰三角形的性质可先证得E为CD的中点,再由三角形中位线定理可得EF=$\frac{1}{2}$BD,又可证明BD=AB-AD=AB-AC,可证得结论.
解答 证明:
∵AD=AC,AE⊥CD,
∴E为CD中点,且F为BC中点,
∴EF=$\frac{1}{2}$BD,
又BD=AB-AD=AB-AC,
∴EF=$\frac{1}{2}$(AB-AC).
点评 本题主要考查等腰三角形的性质和三角形中位线定理,由条件先证明EF为△BCD的中位线是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
3. 通过平移后可以得到的图的是( )
通过平移后可以得到的图的是( )
 通过平移后可以得到的图的是( )
通过平移后可以得到的图的是( )| A. |  | B. |  | C. |  | D. |  |
4.下列现象:(1)钟表钟摆的摆动;(2)气球的升空运动;(3)摩天轮的转动.其中属于旋转的是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | 只有(3) |
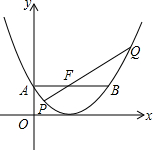 如图,已知抛物线C1:y1=$\frac{1}{4}$x2-x+1,点F(2,1).
如图,已知抛物线C1:y1=$\frac{1}{4}$x2-x+1,点F(2,1).