题目内容
 解不等式组,并把它的解集在数轴上表示出来.
解不等式组,并把它的解集在数轴上表示出来.
|
考点:解一元一次不等式组,在数轴上表示不等式的解集
专题:
分析:首先解每个不等式,两个不等式解集的公共部分就是不等式组的解集,然后然后在数轴上表示即可.
解答:解:
,
解不等式①得:x<2
解不等式②得:x≥-1,
在同一数轴上分别表示出它们的解集

所以原不等式组的解集为:-1≤x<2.
|
解不等式①得:x<2
解不等式②得:x≥-1,
在同一数轴上分别表示出它们的解集

所以原不等式组的解集为:-1≤x<2.
点评:本题考查不等式组的解法,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
相关题目
下列计算中正确的是( )
| A、-9-4=-5 | ||||
B、1÷(-2
| ||||
| C、(-4)3=-12 | ||||
| D、-|-2|=-2 |
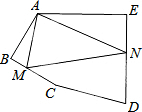 如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )| A、90° | B、100° |
| C、110° | D、120° |
 如图,在平面直角坐标系中,A(6,0)、B(6,2)、C(0,2)、D(1,2),点P为线段OA上一点,且∠BPD=90°,则点P的坐标为
如图,在平面直角坐标系中,A(6,0)、B(6,2)、C(0,2)、D(1,2),点P为线段OA上一点,且∠BPD=90°,则点P的坐标为