题目内容
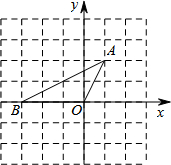 如图,把直角坐标系xoy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.
如图,把直角坐标系xoy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.(1)画出△OA′B′;
(2)点A的坐标是(
(3)若点P在y轴上,且PA+PA′的值最小,则点P的坐标是(
考点:作图-旋转变换,轴对称-最短路线问题
专题:作图题
分析:(1)根据网格结构找出点A、B旋转后的对应点A′、B′的位置,再与点O顺次连接即可;
(2)根据平面直角坐标系写出点A、A′的坐标即可;
(3)先找出点A关于y轴的对称点A″的位置,连接A′A″与y轴相交,根据轴对称确定最短路线问题,点P即为所求作的点P,再根据图形写出点P的坐标即可.
(2)根据平面直角坐标系写出点A、A′的坐标即可;
(3)先找出点A关于y轴的对称点A″的位置,连接A′A″与y轴相交,根据轴对称确定最短路线问题,点P即为所求作的点P,再根据图形写出点P的坐标即可.
解答: 解:(1)△OA′B′如图所示;
解:(1)△OA′B′如图所示;
(2)A(1,2),A′(2,-1);
(3)如图,P(0,1).
故答案为:(2)(1,2),(2,-1);(3)(0,1).
 解:(1)△OA′B′如图所示;
解:(1)△OA′B′如图所示;(2)A(1,2),A′(2,-1);
(3)如图,P(0,1).
故答案为:(2)(1,2),(2,-1);(3)(0,1).
点评:本题考查了利用旋转变换作图,轴对称确定最短路线问题,平面直角坐标系中点的坐标的写法,是基础题,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.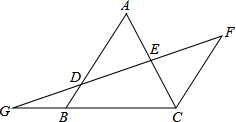 如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G. 某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系. 如图是一副三角板叠放的示意图,则∠α=
如图是一副三角板叠放的示意图,则∠α= 如图,在直角坐标系中,O是原点,已知A(4,3),P是坐标轴上的一点,若以O,A,P三点组成的三角形为等腰三角形,则满足条件的点P共有
如图,在直角坐标系中,O是原点,已知A(4,3),P是坐标轴上的一点,若以O,A,P三点组成的三角形为等腰三角形,则满足条件的点P共有