题目内容
 已知:如图,PA,PB分别与⊙O相切于A,B点,C为⊙O上一点,∠ACB=65°,则∠APB等于_______.
已知:如图,PA,PB分别与⊙O相切于A,B点,C为⊙O上一点,∠ACB=65°,则∠APB等于_______.
- A.65°
- B.50°
- C.45°
- D.40°
B
分析:连接OA,OB.根据圆周角定理和四边形内角和定理求解即可.
解答: 解:连接OA,OB,
解:连接OA,OB,
∵PA、PB切⊙O于点A、B,
∴∠PAO=∠PBO=90°,
由圆周角定理知,∠AOB=2∠ACB=130°,
∴∠APB=360°-∠PAO-∠PBO-∠AOB=360°-90°-90°-130°=50°.
故选B.
点评:本题考查了切线的性质、圆周角定理、以及四边形的内角和为360度.
分析:连接OA,OB.根据圆周角定理和四边形内角和定理求解即可.
解答:
 解:连接OA,OB,
解:连接OA,OB,∵PA、PB切⊙O于点A、B,
∴∠PAO=∠PBO=90°,
由圆周角定理知,∠AOB=2∠ACB=130°,
∴∠APB=360°-∠PAO-∠PBO-∠AOB=360°-90°-90°-130°=50°.
故选B.
点评:本题考查了切线的性质、圆周角定理、以及四边形的内角和为360度.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
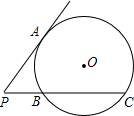 已知:如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=2PB,求
已知:如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=2PB,求 23、已知:如图,PA、PB是⊙O的切线;A、B是切点;连接OA、OB、OP,
23、已知:如图,PA、PB是⊙O的切线;A、B是切点;连接OA、OB、OP, 于点D、E.
于点D、E. 已知:如图,PA,PB分别与⊙O相切于A,B点,C为⊙O上一点,∠ACB=65°,则∠APB等于( )
已知:如图,PA,PB分别与⊙O相切于A,B点,C为⊙O上一点,∠ACB=65°,则∠APB等于( ) 已知:如图,PA切⊙O于A点,PO交⊙O于B点.PA=15cm,PB=9cm.求⊙O的半径长.
已知:如图,PA切⊙O于A点,PO交⊙O于B点.PA=15cm,PB=9cm.求⊙O的半径长.