ЬтФПФкШн
вбжЊжБЯпy=2x+4ЗжБ№гыxжсЁЂyжсНЛгкAЃЌBЃЌгыЫЋЧњЯпy=
дкЕквЛЯѓЯоНЛгкCЃЈ1ЃЌmЃЉЃЎ
ЃЈ1ЃЉЧѓЕуBЁЂЕуCЕФзјБъМАkЕФжЕЃЛ
ЃЈ2ЃЉЮЪдкЫЋЧњЯпy=
ЩЯЧвдкжБЯпy=2x+4ЕФЯТЗНЃЌЪЧЗёДцдкЕуMЃЌЪЙЁїMABЕУУцЛ§ЕШгкЁїABOЕФУцЛ§ЕФ2БЖЃПШєДцдкЃЌЧѓГіMЕуЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕуPЪЧЫЋЧњЯпy=
ЕквЛЯѓЯоЩЯЕФЖЏЕуЃЌQЪЧжБЯпy=2x+4ЩЯЕФЖЏЕуЃЌШєЁїBPQЪЧЕШбќжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЕуPЕФзјБъЃЎ
| k |
| x |
ЃЈ1ЃЉЧѓЕуBЁЂЕуCЕФзјБъМАkЕФжЕЃЛ
ЃЈ2ЃЉЮЪдкЫЋЧњЯпy=
| k |
| x |
ЃЈ3ЃЉЕуPЪЧЫЋЧњЯпy=
| k |
| x |
ПМЕуЃКЗДБШР§КЏЪ§злКЯЬт
зЈЬтЃК
ЗжЮіЃКЃЈ1ЃЉгЩЬтвтПЩжЊBЕуЕФзнзјБъЮЊ4ЃЌCЕуЕФКсзјБъЮЊ1ЃЌЗжБ№ДњШыжБЯпЗНГЬПЩЧѓЕУСНЕуЕФзјБъЃЌдйАбCЕузјБъДњШыЫЋЧњЯпНтЮіЪНПЩЧѓЕУkЕФжЕЃЛ
ЃЈ2ЃЉЁїMABКЭЁїABOжаABЮЊЕзЃЌжЛвЊИпТњзу2БЖЙиЯЕМДПЩЃЌЙ§OзїГіЁїABOЕФABБпЩЯЕФИпЃЌРћгУЖдГЦадЃЌзїГіDЙигкOЕуЕФЖдГЦЕуEЃЌЙ§EКЭABЦНааЕФжБЯпгыЫЋЧњЯпЕФНЛЕуМДЮЊЫљЧѓЕФMЕуЃЌРћгУЧѓНЛЕузјБъЕФЗНЗЈПЩНтГіMЕФзјБъЃЛ
ЃЈ3ЃЉЕБЁЯPBQЮЊжБНЧЪБЃЌЙ§ЕуBЧвДЙжБABЕФжБЯпгыЫЋЧњЯпЕФНЛЕуМДТњзуЬтвтЃЌЕБЁЯPQBЮЊжБНЧЪБЃЌдђЙ§BЕФжБЯпгыжБЯпABЕФМаНЧЮЊ45ЁуМДПЩЃЌЧѓГіЯргІжБЯпЗНГЬЃЌСЊСЂЗНГЬзщЧѓНтМДПЩЃЎ
ЃЈ2ЃЉЁїMABКЭЁїABOжаABЮЊЕзЃЌжЛвЊИпТњзу2БЖЙиЯЕМДПЩЃЌЙ§OзїГіЁїABOЕФABБпЩЯЕФИпЃЌРћгУЖдГЦадЃЌзїГіDЙигкOЕуЕФЖдГЦЕуEЃЌЙ§EКЭABЦНааЕФжБЯпгыЫЋЧњЯпЕФНЛЕуМДЮЊЫљЧѓЕФMЕуЃЌРћгУЧѓНЛЕузјБъЕФЗНЗЈПЩНтГіMЕФзјБъЃЛ
ЃЈ3ЃЉЕБЁЯPBQЮЊжБНЧЪБЃЌЙ§ЕуBЧвДЙжБABЕФжБЯпгыЫЋЧњЯпЕФНЛЕуМДТњзуЬтвтЃЌЕБЁЯPQBЮЊжБНЧЪБЃЌдђЙ§BЕФжБЯпгыжБЯпABЕФМаНЧЮЊ45ЁуМДПЩЃЌЧѓГіЯргІжБЯпЗНГЬЃЌСЊСЂЗНГЬзщЧѓНтМДПЩЃЎ
НтД№ЃКНтЃКЃЈ1ЃЉдкy=2x+4жаЃЌСюx=0ЃЌНтЕУЃКy=4ЃЌ
дђBЕФзјБъЪЧЃЈ0ЃЌ4ЃЉЃЌ
Сюx=1ЃЌНтЕУЃКy=6ЃЌ
дђCЕФзјБъЪЧЃЈ1ЃЌ6ЃЉЃЌ
АбЃЈ1ЃЌ6ЃЉДњШыy=
жаЃЌЕУЃКk=6ЃЛ
ЃЈ2ЃЉдкy=2x+4жаЃЌСюy=0ЃЌНтЕУЃКx=-2ЃЌ
дђAЕФзјБъЪЧЃЈ-2ЃЌ0ЃЉЃЎ
ШчЭМ1ЃЌЙ§OзїODЁЭABгкЕуDЃЌдђжБЯпODЕФНтЮіЪНЪЧy=-
xЃЌ
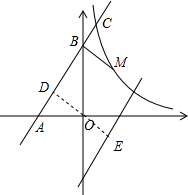
ЭМ1
ИљОнЬтвтЕУЃК
ЃЌ
НтЕУЃК
ЃЌ
дђDЕФзјБъЪЧЃЈ-
ЃЌ
ЃЉЃЌDЙигкOЕФЖдГЦЕуЪЧEЃЈ
ЃЌ-
ЃЉЃЌ
ОЙ§EЧвЦНаагкABЕФжБЯпЕФНтЮіЪНЪЧЃКy=2x+cЃЌдђ-
=
+cЃЌ
НтЕУЃКc=-4ЃЌ
дђНтЮіЪНЪЧy=2x-4ЃЎ
ИљОнЬтвтЕФЃК
ЃЌ
НтЕУЃК
Лђ
ЃЌ
дђMЕФзјБъЪЧЃЈ3ЃЌ2ЃЉЛђЃЈ-1ЃЌ-6ЃЉЃЛ
ЃЈ3ЃЉЕБЁЯPBQ=90ЁуЪБЃЌдђгаBPЁЭABЃЌ
ШчЭМ2ЃЌЙ§ЕуBзїBPЁЭABЃЌНЛЫЋЧњЯпгкЕуPЃЌ
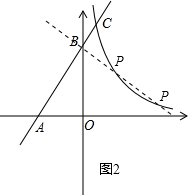
ДЫЪБдкжБЯпABЩЯДцдкТњзуЬѕМўЕФQЕуЃЌ
ДЫЪБжБЯпBPЗНГЬЮЊЃКy=-
x+4ЃЌ
СЊСЂЫЋЧњЯпЗНГЬЕУЃК
ЃЌ
НтЕУЃК
Лђ
ЃЌМДДЫЪБPЕуЕФзјБъЮЊЃЈ2ЃЌ3ЃЉЛђЃЈ1ЃЌ6ЃЉЃЛ
ЕБЁЯBQP=90ЁуЪБЃЌШчЭМ3ЃЌЙ§BЕузїжБЯпBPЃЌЪЙжБЯпBPгыжБЯпABЕФМаНЧЮЊ45ЁуЃЌНЛЫЋЧњЯпгкЕуPЃЌНЛxжсгкЕуDЃЌДЫЪБдкжБЯпABЩЯДцдкТњзуЬѕМўЕФQЕуЃЌ
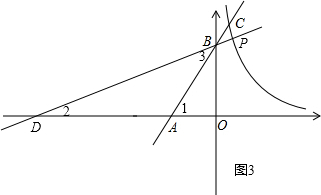
дђЁЯ1=ЁЯ2+ЁЯ3=ЁЯ2+45ЁуЃЌ
ЫљвдtanЁЯ1=tanЃЈЁЯ2+45ЁуЃЉ=
ЃЌ
гжtanЁЯ1=
=
=2ЃЌЫљвд
=2ЃЌ
НтЕУtanЁЯ1=
ЃЌЫљвджБЯпBPЕФЗНГЬЮЊЃКy=
x+4ЃЌ
СЊСЂЫЋЧњЯпЗНГЬЕУЃК
ЃЌ
НтЕУЃК
Лђ
ЃЈвђЮЊPЕудкЕквЛЯѓЯоЃЌЙЪЩсШЅЃЉЃЌ
ДЫЪБPЕуЕФзјБъЮЊЃЈ3
-6ЃЌ
+2ЃЉЃЛ
ЕБЁЯBPQ=90ЁуЪБЃЌЭЌРэПЩЧѓЕУPЕузјБъШдЮЊЃЈ3
-6ЃЌ
+2ЃЉЃЛ
злЩЯПЩжЊТњзуЬѕМўЕФPЕуЕФзјБъЮЊЃКЃЈ2ЃЌ3ЃЉЛђЃЈ1ЃЌ6ЃЉЛђЃЈ3
-6ЃЌ
+2ЃЉЃЎ
дђBЕФзјБъЪЧЃЈ0ЃЌ4ЃЉЃЌ
Сюx=1ЃЌНтЕУЃКy=6ЃЌ
дђCЕФзјБъЪЧЃЈ1ЃЌ6ЃЉЃЌ
АбЃЈ1ЃЌ6ЃЉДњШыy=
| k |
| x |
ЃЈ2ЃЉдкy=2x+4жаЃЌСюy=0ЃЌНтЕУЃКx=-2ЃЌ
дђAЕФзјБъЪЧЃЈ-2ЃЌ0ЃЉЃЎ
ШчЭМ1ЃЌЙ§OзїODЁЭABгкЕуDЃЌдђжБЯпODЕФНтЮіЪНЪЧy=-
| 1 |
| 2 |

ЭМ1
ИљОнЬтвтЕУЃК
|
НтЕУЃК
|
дђDЕФзјБъЪЧЃЈ-
| 8 |
| 5 |
| 4 |
| 5 |
| 8 |
| 5 |
| 4 |
| 5 |
ОЙ§EЧвЦНаагкABЕФжБЯпЕФНтЮіЪНЪЧЃКy=2x+cЃЌдђ-
| 4 |
| 5 |
| 16 |
| 5 |
НтЕУЃКc=-4ЃЌ
дђНтЮіЪНЪЧy=2x-4ЃЎ
ИљОнЬтвтЕФЃК
|
НтЕУЃК
|
|
дђMЕФзјБъЪЧЃЈ3ЃЌ2ЃЉЛђЃЈ-1ЃЌ-6ЃЉЃЛ
ЃЈ3ЃЉЕБЁЯPBQ=90ЁуЪБЃЌдђгаBPЁЭABЃЌ
ШчЭМ2ЃЌЙ§ЕуBзїBPЁЭABЃЌНЛЫЋЧњЯпгкЕуPЃЌ

ДЫЪБдкжБЯпABЩЯДцдкТњзуЬѕМўЕФQЕуЃЌ
ДЫЪБжБЯпBPЗНГЬЮЊЃКy=-
| 1 |
| 2 |
СЊСЂЫЋЧњЯпЗНГЬЕУЃК
|
НтЕУЃК
|
|
ЕБЁЯBQP=90ЁуЪБЃЌШчЭМ3ЃЌЙ§BЕузїжБЯпBPЃЌЪЙжБЯпBPгыжБЯпABЕФМаНЧЮЊ45ЁуЃЌНЛЫЋЧњЯпгкЕуPЃЌНЛxжсгкЕуDЃЌДЫЪБдкжБЯпABЩЯДцдкТњзуЬѕМўЕФQЕуЃЌ

дђЁЯ1=ЁЯ2+ЁЯ3=ЁЯ2+45ЁуЃЌ
ЫљвдtanЁЯ1=tanЃЈЁЯ2+45ЁуЃЉ=
| 1+tanЁЯ2 |
| 1-tanЁЯ2 |
гжtanЁЯ1=
| OB |
| OA |
| 4 |
| 2 |
| 1+tanЁЯ2 |
| 1-tanЁЯ2 |
НтЕУtanЁЯ1=
| 1 |
| 3 |
| 1 |
| 3 |
СЊСЂЫЋЧњЯпЗНГЬЕУЃК
|
НтЕУЃК
|
|
ДЫЪБPЕуЕФзјБъЮЊЃЈ3
| 6 |
| 6 |
ЕБЁЯBPQ=90ЁуЪБЃЌЭЌРэПЩЧѓЕУPЕузјБъШдЮЊЃЈ3
| 6 |
| 6 |
злЩЯПЩжЊТњзуЬѕМўЕФPЕуЕФзјБъЮЊЃКЃЈ2ЃЌ3ЃЉЛђЃЈ1ЃЌ6ЃЉЛђЃЈ3
| 6 |
| 6 |
ЕуЦРЃКБОЬтжївЊПМВщЗДБШР§КЏЪ§гывЛДЮКЏЪ§злКЯгІгУЃЌдкЕкЃЈ2ЃЉЁЂЃЈ3ЃЉжаШЗЖЈГіЫљЧѓЕуЕФЮЛжУЪЧНтЬтЕФЙиМќЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
ХзЮяЯпy=-ЃЈx-2ЃЉ2+3ЕФЖЅЕузјБъЮЊЃЈЁЁЁЁЃЉ
| AЁЂЃЈ0ЃЌ3ЃЉ |
| BЁЂЃЈ-2ЃЌ3ЃЉ |
| CЁЂЃЈ0ЃЌ1ЃЉ |
| DЁЂЃЈ2ЃЌ3ЃЉ |
ЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
| AЁЂЕЙЪ§КЭЫќБОЩэЯрЕШЕФЪ§ЃЌжЛга1КЭ-1 |
| BЁЂЯрЗДЪ§гыБОЩэЯрЕШЕФЪ§жЛга0 |
| CЁЂСЂЗНЕШгкЫќБОЩэЕФЪ§жЛга0ЁЂ1КЭ-1 |
| DЁЂОјЖджЕЕШгкБОЩэЕФЪ§ЪЧе§Ъ§ |
МЦЫу-ЃЈ-3ЃЉ2ЕФНсЙћЪЧЃЈЁЁЁЁЃЉ
| AЁЂ6 | BЁЂ-6 | CЁЂ9 | DЁЂ-9 |
 вбжЊЃКШчЭМЃЌдкЕШБпШ§НЧаЮABCжаЃЌMЁЂNЗжБ№ЪЧABЁЂACЕФжаЕуЃЌDЪЧMNЩЯШЮвтвЛЕуЃЌCDЁЂBDЕФбгГЄЯпЗжБ№гыABЁЂACНЛгкFЁЂEЃЌШє
вбжЊЃКШчЭМЃЌдкЕШБпШ§НЧаЮABCжаЃЌMЁЂNЗжБ№ЪЧABЁЂACЕФжаЕуЃЌDЪЧMNЩЯШЮвтвЛЕуЃЌCDЁЂBDЕФбгГЄЯпЗжБ№гыABЁЂACНЛгкFЁЂEЃЌШє