题目内容
7.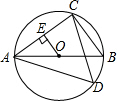 如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.
如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.(1)求sin∠ADC的值;
(2)如果OE⊥AC,垂足为E,求OE的长.
分析 (1)根据直径所对的圆周角是直角证明△ABC是直角三角形,根据题意求出∠BAC=30°和∠ABC=60°,根据∠ABC=∠ADC,得到答案;
(2)根据垂径定理和三角形的中位线定理即可求出OE的长.
解答 解:(1)∵AB是⊙O直径,
∴∠ACB=90°,
∵AB=6,BC=3,
∴∠BAC=30°,∠ABC=60°,
∵∠ABC=∠ADC,
∴Sin∠ADC=$\frac{\sqrt{3}}{2}$;
(2)∵OE⊥AC,
∴AE=EC,
∵O是⊙O的圆心,
∴OA=OB,
∴OE=$\frac{1}{2}$BC=1.5.
点评 本题考查的是垂径定理、解直角三角形和圆周角定理的应用,掌握直径所对的圆周角是直角和特殊角的三角函数值是解题的关键.

练习册系列答案
相关题目
2.点P与点Q(-3,2)关于原点对称,则点P的坐标是( )
| A. | (-3,2) | B. | (2,-3) | C. | (3,-2) | D. | (-2,3) |
12.在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的夹角为α,则用[ρ,α]表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为(1,1),则其极坐标为[$\sqrt{2}$,45°].若点Q的极坐标为[4,120°],则点Q的坐标为( )
| A. | $(-\right.2,2\sqrt{3}\left.{\;})$ | B. | $(-2,-2\sqrt{3})$ | C. | (2$\sqrt{3}$,2) | D. | (2,2) |
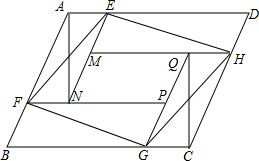 如图,有八个全等的三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ,连接EF、GH得到四边形EFGH,设S四边形ABCD=S1,S四边形EFGH=S2,S四边形MNPQ=S3,若S1+S2+S3=10,则S2=$\frac{10}{3}$.
如图,有八个全等的三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ,连接EF、GH得到四边形EFGH,设S四边形ABCD=S1,S四边形EFGH=S2,S四边形MNPQ=S3,若S1+S2+S3=10,则S2=$\frac{10}{3}$.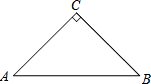 如图,等腰Rt△ABC中,AC=BC,AB=2,将线段AB绕A点逆时针方向旋转,B点的对应点为D,若CD∥AB,则CD的长为$\sqrt{3}$+1或$\sqrt{3}$-1.
如图,等腰Rt△ABC中,AC=BC,AB=2,将线段AB绕A点逆时针方向旋转,B点的对应点为D,若CD∥AB,则CD的长为$\sqrt{3}$+1或$\sqrt{3}$-1. 如图所示,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,问:∠1和∠2相等吗?请说明理由.
如图所示,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,问:∠1和∠2相等吗?请说明理由.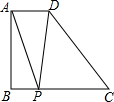 如图,已知梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=DC=5,点P为BC边上一个动点,连接PA、PD,则△PAD周长的最小值是2$\sqrt{17}$+2.
如图,已知梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=DC=5,点P为BC边上一个动点,连接PA、PD,则△PAD周长的最小值是2$\sqrt{17}$+2. 如图所示,以AB为对称轴,画出已知图形△CDE的轴对称图形.
如图所示,以AB为对称轴,画出已知图形△CDE的轴对称图形.