题目内容
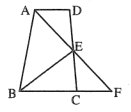
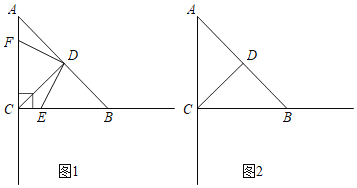
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 的内心,
的内心,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连
,连![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,①求
,①求![]() 的长; ②求
的长; ②求![]() 的面积.
的面积.
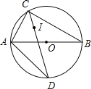
【答案】(1)证明见解析;(2)①10;②24.
【解析】
(1)连接AI,运用内切圆的性质及三角形外角的性质问题即可解决.
(2)①连接BD,证明DB=DI,进而DB=DA;由勾股定理即可求得AB的长;
②作辅助线,构造相似三角形,求得△ABC的AB边上的高,即可解决问题.
(1)连接AI.
∵点I是△ABC(AC<AB)的内心,∴∠CAI=∠BAI,∠ACI=∠BCI.
∵∠DAB=∠BCI,∴∠DAB=∠ACI,∴∠DAB+∠OAI=∠ACI+∠CAI.
∵∠AID=∠ACI+∠CAI,∠DAI=∠DAB+∠OAI,∴∠AID=∠DAI,∴DA=DI.
(2)连接BI,OD,BD,过点C作CP⊥AB于点P.
①类比(1)中的方法,同理可证DB=DI,∴DA=DB=DI=![]() .
.
∵AB是⊙O的直径,∴∠ADB=90°,由勾股定理得:
![]() =10,即AB的长为10.
=10,即AB的长为10.
②∵∠ACD=∠BCD,∠DAQ=∠BCD,∴∠ACD=∠DAQ,而∠ADC=∠ADQ,∴△ADC≌△QDA,∴![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() .
.
∵DA=DB,AO=BO,∴DO⊥AB,![]() .
.
而CP⊥AB,∴△CPQ∽△DOQ,∴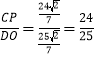 ,∴CP=
,∴CP=![]() =
=![]() ,∴
,∴![]() .即△ABC的面积为24.
.即△ABC的面积为24.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目