Question

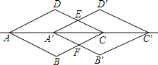
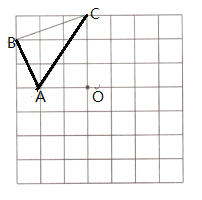
【题目】在正方形网格图中，若每个小正方形的边长是1，与关于点对称．

（1）画出．

（2）与的位置关系是 ．

（3）点在直线上，的最小值是 ．

Answer 1

【答案】（1）见解析；（2）A1B1∥AB；（3）

【解析】

（1）分别描出A、B、C关于点O的对称点，连接即可得到；

（2）连接A A1，B B1，由对称性判定△AOB≌△A1OB1，得出∠ABO=∠A1B1O，即可判定A1B1∥AB；

（3）连接BA1，交OC于点P，当B、P、A1三点在一条直线上时，取得最小值，利用勾股定理即可得解.

（1）如图所示：

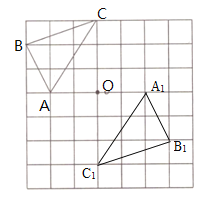
（2）连接A A1，B B1，如图所示：

由对称性，得OA=OA1，OB=OB1，

∵∠AOB=∠A1OB1

∴△AOB≌△A1OB1（SAS）

∴∠ABO=∠A1B1O

∴A1B1∥AB；

（3）连接BA1，交OC于点P，如图所示：

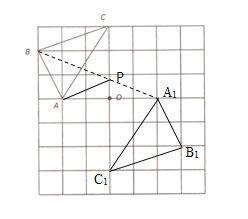
当B、P、A1三点在一条直线上时，取得最小值

∴